Interested Article - Изотоксальная фигура

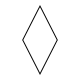
Многогранник , многоугольник или мозаика является изотоксальным или рёберно транзитивным , если его симметрии действуют транзитивно на его рёбрах. Неформально это означает, что имеется только один вид рёбер у объекта — если даны два ребра, существует параллельный перенос, вращение и/или зеркальное отражение, переводящее одно ребро в другое, не меняя область, занимаемую объектом.

Термин изотоксальный происходит от греческого τοξον , означающего дуга .

Изотоксальные многоугольники

Изотоксальный многоугольник всегда является равносторонним , но не все равносторонние многоугольники изотоксальны. Двойственные изотоксальным многоугольникам являются изогональными многоугольниками .

В общем случае изотоксальный 2n -угольник будет иметь D _n (*nn) диэдральную симметрию . Ромб является рёберно транзитивным многоугольником с симметрией D ₂ (*22).

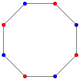
Все правильные многоугольники ( правильный треугольник , квадрат , и т. д.) изотоксальны, имея удвоенный минимальный порядок симметрии — правильный n -угольник имеет D _n (*nn) диэдральную симметрию. Правильный 2 n -угольник является вершинно транзитивным многоугольником и его вершины могут быть помечены поочерёдно двумя цветами, что удаляет осевую симметрию через середину рёбер.

Примеры изотоксальных многоугольников
D ₂ (*22)	D ₃ (*33)			D ₄ (*44)		D ₅ (*55)
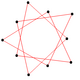
Ромб	Равносторонний треугольник	Вогнутый шестиугольник	Самопересекающийся шестиугольник	Выпуклый восьмиугольник		Правильный пятиугольник	Самопересекающаяся (правильная) пентаграмма	Самопересекающаяся

Рёберно-транзитивные многогранники и мозаики

Правильные многогранники являются изоэдральными (гране транзитивными), изогональными (вершинно транзитивными) и изотоксальными (рёберно транзитивными). Квазиправильные многогранники являются изогональными и изотоксальными, но не изоэдральными. Их двойственные многогранники изоэдральны и изотоксальны, но не изогональны.

Примеры
Квазиправильный многогранник	Квазиправильный двойственный многогранник	Квазиправильный звёздчатый многогранник	Квазиправильный двойственный звёздчатый многогранник	Квазиправильная мозаика	Квазиправильная двойственная мозаика
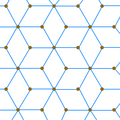
Кубооктаэдр является изогональным и изотоксальным многогранником	Ромбододекаэдр является изоэдральным и изотоксальным многогранником	Большой икосододекаэдр является изогональным и изотоксальным звёздчатым многогранником	Большой ромбический тридцатигранник	Тришестиугольная мозаика является изогональной и изотоксальной мозаикой	Ромбическая мозаика является изоэдральной и изотоксальной мозаикой с симметрией p6m (*632).

Не любой многогранник или 2-мерная мозаика , состоящие из правильных многоугольников , изотоксален. Например, усечённый икосаэдр (знакомый нам по футбольному мячу) имеет два типа рёбер — шестиугольник-шестиугольник и шестиугольник-пятиугольник и нет возможности симметрией перевести ребро шестиугольник-шестиугольник в шестиугольник-пятиугольник.

Изотоксальный многоугольник имеет те же самые диэдральные углы для всех рёбер.

Существует девять выпуклых рёберно транзитивных многогранников, образованных из правильных многогранников , 8, образованных из многогранников Кеплера — Пуансо , и ещё шесть являются квазиправильными звёздчатыми многогранниками (3 | p q) и их двойственными.

Существует 5 многоугольных рёберно транзитивных мозаик на евклидовой плоскости и бесконечно много на гиперболической плоскости, включая построения Уитхофф из правильных гиперболических мозаик {p, q} и неправильных (p q r) групп.

См. также

Примечания

Литература

P. Cromwell. . — United Kingdom: Cambridge University Press, 1997. — С. 371. — ISBN 0-521-55432-2 .
Grünbaum B. , Shephard G.C. 6.4 Isotoxal tilings // Tilings and Patterns. — New York: W. H. Freeman & Co., 1987. — С. 309—321. — ISBN 0-7167-1193-1 .
Coxeter H. S. M. , Longuet-Higgins M. S., Miller J. C. P. Uniform polyhedra // Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. — The Royal Society, 1954. — Т. 246 , вып. 916 . — С. 401–450 . — ISSN . — doi : . — JSTOR .