Interested Article - Десятиугольник

- 2020-12-18
- 1
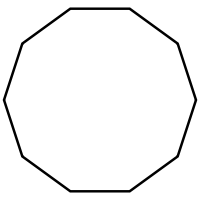
| Правильный десятиугольник | |
|---|---|
|
|
| Сторон и вершин | 10 |
| Символ Шлефли | {10} |
| Внутренний угол | 144° |
| Симметрия | Диэдрическая ( ), порядок 20. |
Десятиуго́льник (правильный десятиугольник — декагон) — многоугольник с десятью углами и десятью сторонами.
Правильный десятиугольник
У правильного десятиугольника все стороны равной длины, и каждый внутренний угол составляет 144°.
Площадь правильного десятиугольника равна (t — длина стороны):
Альтернативная формула , где d - расстояние между параллельными сторонами или диаметр вписанной окружности. В тригонометрических функциях он выражается так:
и может быть представлен в радикалах как
Сторона правильного десятиугольника, вписанного в единичную окружность , равна , где - золотое сечение .
Радиус описанной окружности десятиугольника равен
а радиус вписанной окружности
Построение
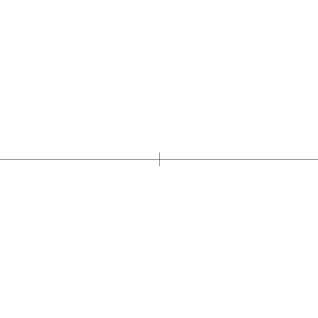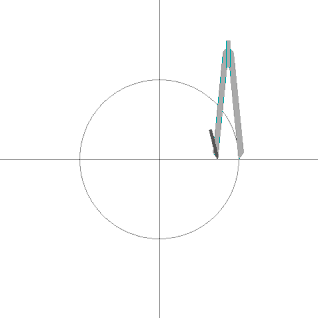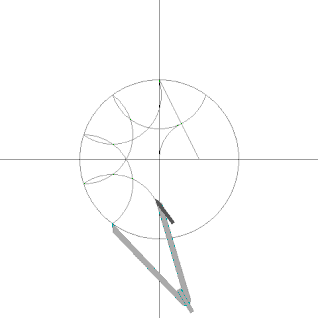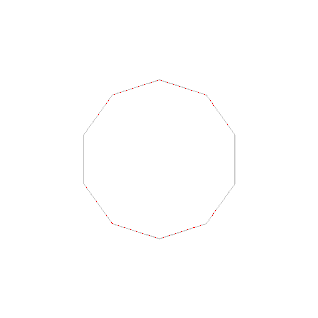
По теореме Гаусса — Ванцеля правильный десятиугольник возможно построить, используя лишь циркуль и линейку . На диаграмме показано одно из таких построений. Иначе его можно построить следующим образом:
- Построить сначала правильный пятиугольник .
- Соединить все его вершины с центром описанной окружности прямыми до пересечения с этой же окружностью на противоположной стороне. В этих точках пересечения и находятся остальные пять вершин десятиугольника.
- Соединить по порядку вершины пятиугольника и пять точек, найденные шагом ранее. Искомый десятиугольник построен.
Разбиение правильного десятиугольника
Гарольдом Коксетером было доказано, что правильный -угольник (в общем случае - -угольный зоногон ) можно разбить на ромбов. Для декагона , так что он может быть разбит на 10 ромбов.
| Разбиение правильного десятиугольника | |
|---|---|

|
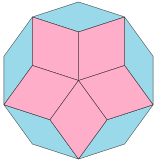
|
Пространственный десятиугольник
| Правильные пространственные десятиугольники | ||
|---|---|---|
| {5}#{ } | {5/2}#{ } | {5/3}#{ } |

|
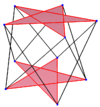
Пентаграммная антипризма |

Пентаграммная антипризма с перекрёстом |
Пространственный десятиугольник — это пространственный многоугольник с десятью рёбрами и вершинами, но не лежащими в одной плоскости. У пространственного зиг-заг десятиугольника вершины чередуются между двумя параллельными плоскостями.
У правильного пространственного десятиугольника все рёбра равны. В трёхмерном пространстве это зиг-заг пространственный декагон, он может быть обнаружен среди рёбер и вершин пентагональной антипризмы, пентаграммной антипризмы, пентаграммной перекрещивающейся антипризмы с той же D 5d [2 + ,10] симметрией порядка 20.
Его также можно найти в некоторых выпуклых многогранниках с икосаэдрической симметрией. Многоугольники по периметру этих проекций (см. ниже) это пространственные десятиугольники.
| Ортогональные проекции многогранников | |||
|---|---|---|---|
 Додекаэдр
Додекаэдр
|
 Икосаэдр
Икосаэдр
|
 Икосододекаэдр
Икосододекаэдр
|
 Ромботриаконтаэдр
Ромботриаконтаэдр
|
Многоугольники Петри
Правильный пространственный десятиугольник — это многоугольник Петри для многих многогранников высших размерностей, как показано на этих ортогональных проекциях на различных плоскостях Коксетера .
| A 9 | D 6 | B 5 | ||
|---|---|---|---|---|
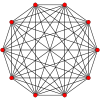 9-симплекс
9-симплекс
|
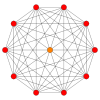 4
11
4
11
|
 1
31
1
31
|
 5-ортоплекс
5-ортоплекс
|
 5-куб
5-куб
|
Примечания
- от 1 марта 2021 на Wayback Machine , §225.
Ссылки
- Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
-
 На
Викискладе
есть медиафайлы по теме
На
Викискладе
есть медиафайлы по теме
- 2020-12-18
- 1












