Правильный двенадцатиугольник
Углы	12
Символ Шлефли	{12} t{6}

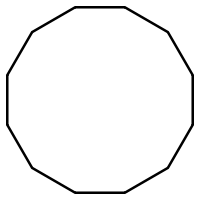
Двенадцатиуго́льник , додекаго́н ( греч. δώδεκα — двенадцать и греч. γωνία — угол ) — многоугольник с 12 углами и 12 сторонами. Как правило, двенадцатиугольником называют правильный многоугольник, то есть такой, у которого все стороны и все углы равны (в случае двенадцатиугольника углы равны 150°). Правильный двенадцатиугольник используется в некоторых странах в качестве формы для монет .

Правильный двенадцатиугольник

Площадь правильного двенадцатиугольника со стороной a находится по формуле:

${\displaystyle {\begin{aligned}A&=3\cos \left({\frac {\pi }{12}}\right)a^{2}=3\left(2+{\sqrt {3}}\right)a^{2}&\simeq 11.196152422706632\,a^{2}.\end{aligned}}}$

Или, при радиусе описанной окружности R :

${\displaystyle A=6\sin \left({\frac {\pi }{6}}\right)R^{2}=3R^{2}.}$

Или, при радиусе вписанной окружности r :

${\displaystyle {\begin{aligned}A&=12\tan \left({\frac {\pi }{12}}\right)r^{2}=12\left(2-{\sqrt {3}}\right)r^{2}&\simeq 3.2153903091734737\,r^{2}.\end{aligned}}}$

Монеты

Схема построения правильного двенадцатиугольника с помощью циркуля и линейки

Правильный двенадцатиугольник, согласно теореме Гаусса — Ванцеля , относится к многоугольникам, которые можно построить с помощью циркуля и линейки .

Разбиение правильного двенадцатиугольника

Гарольдом Коксетером было доказано, что правильный ${\displaystyle 2m}$ -угольник (в общем случае - ${\displaystyle 2m}$ -угольный зоногон ) можно разбить на ${\displaystyle {\frac {m(m-1)}{2}}}$ ромбов. Для двенадцатиугольника ${\displaystyle m=6}$ , так что он может быть разбит на 15 ромбов.

Разбиение правильного двенадцатиугольника

См. также

• Последовательность двенадцатиугольника

Ссылки

• от 28 июля 2011 на Wayback Machine на MathWorld
• от 25 ноября 2010 на Wayback Machine

Это заготовка статьи по математике . Помогите Википедии, дополнив её.