Теорема Стокса
- 1 year ago
- 0
- 0
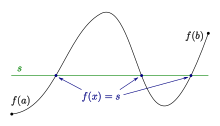
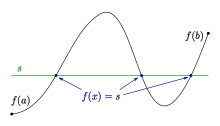
Теорема о промежуточном значении (или Теоре́ма Больца́но — Коши́ ) утверждает, что если непрерывная функция, определённая на вещественном промежутке , принимает два значения, то она принимает и любое значение между ними.
Пусть дана непрерывная функция на отрезке Пусть также и без ограничения общности предположим, что Тогда для любого существует такое, что .
Рассмотрим функцию Она непрерывна на отрезке и , Покажем, что существует такая точка , что Разделим отрезок точкой на два равных по длине отрезка, тогда либо и нужная точка найдена, либо и тогда на концах одного из полученных промежутков функция принимает значения разных знаков (на левом конце меньше нуля, на правом больше).
Обозначив полученный отрезок , разделим его снова на два равных по длине отрезка и т.д. Тогда, либо через конечное число шагов придем к искомой точке , либо получим последовательность вложенных отрезков по длине стремящихся к нулю и таких, что
Пусть - общая точка всех отрезков (согласно принципу Кантора , она существует и единственна) , Тогда и в силу непрерывности функции
Поскольку
получим, что
Теорема Больцано — Коши допускает обобщение на более общие топологические пространства . Всякая непрерывная функция , определенная на связном топологическом пространстве, принимающая какие-либо два значения, принимает и любое лежащее между ними. Формальная запись: пусть дано связное топологическое пространство и функция Пусть и Тогда
В такой формулировке теорема является частным случаем теоремы о том, что образ связного множества при непрерывном отображении связен.
Теорема была сформулирована независимо Больцано в 1817 и Коши в 1821.