Токарь
- 1 year ago
- 0
- 0

Пло́тность то́ка — векторная физическая величина , характеризующая плотность потока электрического заряда в рассматриваемой точке. В СИ измеряется в Кл/м 2 /c или, что то же самое, А/м 2 .
Если все носители заряда имеют одинаковый заряд , плотность тока вычисляется по формуле
где (м -3 ) — концентрация носителей, а — средняя скорость их движения. В более сложных случаях производится суммирование по носителям разных сортов.
Плотность тока имеет технический смысл силы электрического тока , протекающего через элемент поверхности единичной площади . При равномерном распределении плотности тока и сонаправленности её с нормалью к поверхности, через которую протекает ток, для величины вектора плотности тока выполняется:
где I — сила тока через поперечное сечение проводника площадью S . Иногда говорится о скалярной плотности тока, в таких случаях под ней подразумевается величина в формуле выше.
В простейшем предположении, что все носители тока (заряженные частицы) двигаются с одинаковым вектором скорости и имеют одинаковые заряды (такое предположение может иногда быть приближенно верным; оно позволяет лучше всего понять физический смысл плотности тока), а концентрация их ,
где — плотность заряда этих носителей. Направление вектора соответствует направлению вектора скорости , с которой движутся заряды , создающие ток, если q положительно. В реальности даже носители одного типа движутся вообще говоря и как правило с различными скоростями. Тогда под следует понимать среднюю скорость.
В сложных системах (с различными типами носителей заряда, например, в плазме или электролитах)
то есть вектор плотности тока есть сумма плотностей тока по всем разновидностям (сортам) подвижных носителей; где — концентрация частиц , — заряд частицы, — вектор средней скорости частиц -го сорта.
Выражение для общего случая может быть записано также через сумму по всем индивидуальным частицам из некоторого малого объёма , содержащего рассматриваемую точку:
Сама формула почти совпадает с формулой, приведенной чуть выше, но теперь индекс суммирования i означает не номер типа частицы, а номер каждой индивидуальной частицы, не важно, имеют они одинаковые заряды или разные, при этом концентрации оказываются уже не нужны.
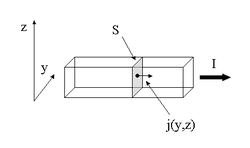
В общем случае сила тока (полный ток) может быть рассчитана исходя из плотности тока по формуле
где — нормальная (ортогональная) составляющая вектора плотности тока по отношению к элементу поверхности площадью ; вектор — специально вводимый вектор элемента поверхности, ортогональный элементарной площадке и имеющий абсолютную величину, равную её площади, позволяющий записать подынтегральное выражение как обычное скалярное произведение. Обратное нахождение плотности тока по известной силе тока невозможно; в предположении равноплотного токопротекания перпендикулярно площадке будет .
Сила тока представляет собой поток вектора плотности тока через заданную фиксированную поверхность. Часто в качестве такой поверхности рассматривается поперечное сечение проводника.
Величиной плотности тока обычно оперируют при решении физических задач, в которых анализируется движение заряженных носителей ( электронов , ионов , дырок и других). Напротив, использование силы тока удобнее в задачах электротехники , особенно когда рассматриваются электрические цепи с сосредоточенными элементами.
Величина плотности тока фигурирует в ряде важнейших формул классической электродинамики , некоторые из них представлены ниже.
Плотность тока в явном виде входит в одно из четырёх уравнений Максвелла , а именно в уравнение для ротора напряжённости магнитного поля
физическое содержание которого в том, что вихревое магнитное поле порождается электрическим током, а также изменением электрической индукции ; значок обозначает частную производную (по времени ). Это уравнение приведено здесь в системе СИ.
Уравнение непрерывности выводится из уравнений Максвелла и утверждает, что дивергенция плотности тока равна изменению плотности заряда со знаком минус, то есть
В линейной и изотропной проводящей среде плотность тока связана с напряжённостью электрического поля в данной точке по закону Ома (в дифференциальной форме):
где — удельная проводимость среды, — напряжённость электрического поля. Или:
где — удельное сопротивление .
В линейной анизотропной среде имеет место такое же соотношение, однако удельная электропроводность в этом случае, вообще говоря, должна рассматриваться как тензор, а умножение на неё — как умножение вектора на матрицу.
Работа, совершаемая электрическим полем над носителями тока, характеризуется плотностью мощности [энергия/(время•объем)]:
где точкой обозначено скалярное произведение .
Чаще всего эта мощность рассеивается в среду в виде тепла, но вообще говоря она связана с полной работой электрического поля и часть её может переходить в другие виды энергии, например такие, как энергия того или иного вида излучения, механическая работа (особенно — в электродвигателях) и т. д.
С использованием закона Ома формула для изотропной среды переписывается как
где и — скаляры. Для анизотропного случая будет
где подразумевается матричное умножение (справа налево) вектора-столбца на матрицу и на вектор-строку, а тензор и тензор порождают соответствующие квадратичные формы .
В теории относительности вводится четырёхвектор плотности тока (4-ток), составленный из объёмной плотности заряда и 3-вектора плотности тока
где — скорость света .
4-ток является прямым и естественным обобщением понятия плотности тока на четырёхмерный пространственно-временной формализм и позволяет, в частности, записывать уравнения электродинамики в ковариантном виде.