Interested Article - Абсолютно чёрное тело

- 2021-02-25
- 2

Абсолю́тно чёрное те́ло — физическое тело , которое при любой температуре поглощает всё падающее на него электромагнитное излучение во всех диапазонах .
Таким образом, у абсолютно чёрного тела поглощательная способность (отношение поглощённой энергии к энергии падающего излучения) равна 1 для излучения всех частот, направлений распространения и поляризаций .
Несмотря на название, абсолютно чёрное тело само может испускать электромагнитное излучение любой частоты и визуально иметь . Спектр излучения абсолютно чёрного тела определяется только его температурой .
Важность абсолютно чёрного тела в теории теплового излучения обусловлена тем, что вопрос о спектре равновесного теплового излучения тел любого цвета и коэффициента отражения сводится методами классической термодинамики к вопросу об излучении абсолютно чёрного тела. К концу XIX века проблема излучения абсолютно чёрного тела вышла на первый план.
Спектральная плотность мощности излучения чёрного тела (мощность, излучаемая с поверхности единичной площади в единичном интервале частот в герцах) задаётся формулой Планка
- ,
где — температура, — постоянная Планка , — скорость света, — постоянная Больцмана , — частота электромагнитного излучения.
Среди тел Солнечной системы свойствами абсолютно чёрного тела в наибольшей степени обладает Солнце . Максимум энергии излучения Солнца приходится примерно на длину волны 450 нм , что соответствует температуре наружных слоёв Солнца около 6000 K (если рассматривать Солнце как абсолютно чёрное тело) .
Термин «абсолютно чёрное тело» был введён Густавом Кирхгофом в 1862 году .
Практическая модель абсолютно чёрного тела

Для физических экспериментов и обсуждений, касающихся проблематики абсолютно чёрного тела, используют модельный объект . Он представляет собой кусок непрозрачного материала, имеющий замкнутую полость с изотермическими стенками, к которой ведёт небольшое отверстие. Свет, попадающий внутрь сквозь это отверстие, после многократных отражений будет полностью поглощён, и отверстие снаружи будет выглядеть совершенно чёрным . Но при нагревании этой полости у неё появится собственное видимое излучение. Поскольку излучение, испущенное внутренними стенками полости, прежде чем выйдет (ведь отверстие очень мало), в подавляющей доле случаев претерпит огромное количество новых поглощений и излучений, то можно с уверенностью сказать, что излучение внутри полости находится в термодинамическом равновесии со стенками. (На самом деле, наличие отверстия для этой модели вообще не важно, оно нужно только чтобы подчеркнуть принципиальную наблюдаемость излучения, находящегося внутри; отверстие можно, например, совсем закрыть, и быстро приоткрыть только тогда, когда равновесие уже установилось и проводится измерение.)
Электромагнитное излучение, находящееся в термодинамическом равновесии с абсолютно чёрным телом при данной температуре (например, излучение внутри полости в абсолютно чёрном теле), называется чернотельным (или тепловым равновесным) излучением. Равновесное тепловое излучение однородно, изотропно и неполяризовано, перенос энергии в нём отсутствует, все его характеристики зависят только от температуры абсолютно чёрного тела-излучателя (и, поскольку чернотельное излучение находится в тепловом равновесии с данным телом, эта температура может быть приписана излучению).
Примеры чёрных тел и чернотельного излучения
Близким к единице коэффициентом поглощения обладают сажа и платиновая чернь . Сажа поглощает до 99 % падающего излучения (то есть имеет альбедо , равное 0,01) в видимом диапазоне длин волн , однако инфракрасное излучение поглощается ею значительно хуже.
Наиболее чёрное из всех известных веществ — изобретённая в 2014 году субстанция Vantablack , состоящая из параллельно ориентированных углеродных нанотрубок , — поглощает 99,965 % падающего на него излучения в диапазонах видимого света, микроволн и радиоволн.
Очень близко по своим свойствам к чернотельному так называемое реликтовое излучение , или космический микроволновой фон — заполняющее Вселенную излучение с температурой около 3 K.
Чернотельным является излучение Хокинга (квантовомеханическое испарение чёрных дыр). Это излучение имеет температуру , где — гравитационная постоянная , а — масса чёрной дыры.
Законы излучения абсолютно чёрного тела
Под законами излучения подразумеваются зависимости испускательной способности поверхности тела от частоты ( , Вт/м 2 /Гц) или длины волны ( , Вт/м 2 /м) излучения, а также утверждения, касающиеся особенностей таких зависимостей. Вместо испускательной способности может рассматриваться связанная с ней формулой (где — скорость света ) объёмная спектральная плотность излучения (Дж/м 3 /Гц для или Дж/м 3 /м для ).
Изначально при поиске выражения для закона излучения чёрного тела были применены классические методы, которые дали ряд важных и верных результатов, но полностью решить проблему не позволили. В итоге анализ излучения абсолютно чёрного тела явился одной из предпосылок появления квантовой механики .
Классические законы
Закон Рэлея — Джинса
Попытка описать излучение абсолютно чёрного тела на основе классических принципов термодинамики приводит к закону Рэлея — Джинса ( k — постоянная Больцмана , — температура):
- ,
- .
Формула соответствует эксперименту в длинноволновой области спектра.
Однако, эта формула предполагает неограниченное квадратичное возрастание спектральной плотности с частотой. На практике данный закон означал бы невозможность термодинамического равновесия между веществом и излучением , поскольку согласно ему вся тепловая энергия должна была бы перейти в энергию коротковолнового излучения. Такое гипотетическое явление было названо ультрафиолетовой катастрофой .
Первый закон излучения Вина
В 1893 году Вильгельм Вин , воспользовавшись, помимо классической термодинамики , электромагнитной теорией света , вывел следующую формулу:
- ,
- ,
где f — функция, зависящая исключительно от отношения частоты к температуре. Установить её вид только из термодинамических соображений невозможно.
Первая формула Вина справедлива для всех частот.
Из неё выводится закон смещения Вина (закон максимума) в виде
- ,
где отвечает максимуму функции . Также можно получить закон Стефана — Больцмана :
- ,
где — мощность излучения единицы поверхности тела. Константы могут быть оценены из эксперимента. Для теоретического же их определения требуются методы квантовой механики.
Второй закон излучения Вина
В 1896 году Вин на основе дополнительных предположений вывел второй закон:
- ,
- ,
где C 1 , C 2 — константы. Опыт показывает, что вторая формула Вина справедлива лишь в пределе высоких частот (малых длин волн). Она является частным конкретным случаем первого закона Вина.
Как и в случае закона максимума, константы не могут быть определены только из классических моделей.
Квантовомеханические законы
Закон Планка
По современным представлениям, интенсивность излучения абсолютно чёрного тела в зависимости от частоты и температуры определяется законом Планка :
- .
Здесь приведено выражение как для объёмной спектральной плотности энергии , так и для поверхностной спектральной плотности мощности излучения . Это эквивалентно
- ,
где те же величины представлены как зависимости от длины волны.
Исходя из формулы Планка можно получить формулу Рэлея — Джинса при .
Также было показано, что второй закон Вина следует из закона Планка для больших энергий квантов — и были найдены входящие в закон Вина постоянные C 1 и C 2 . В результате формула второго закона Вина обретает вид
- .
Во всех вышеприведённых выражениях через h обозначена постоянная Планка .
Закон смещения Вина
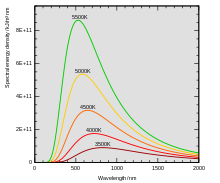
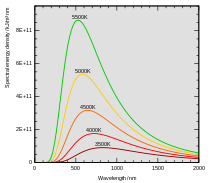
Длина волны, при которой спектральная плотность мощности излучения абсолютно чёрного тела максимальна, определяется законом смещения Вина :
где — температура в кельвинах , а — длина волны, отвечающей максимуму , в метрах . Числовой множитель получается из формулы Планка.
Если считать, что кожа человека близка по свойствам к абсолютно чёрному телу, то максимум спектра излучения при температуре 36 °C (309 K) лежит на длине волны 9400 нм (в инфракрасной области).
Закон Стефана — Больцмана
Закон Стефана — Больцмана гласит, что полная мощность излучения (Вт/м 2 ) абсолютно чёрного тела, то есть интеграл спектральной плотности мощности по всем частотам, приходящаяся на единицу площади поверхности, прямо пропорциональна четвёртой степени температуры тела:
- ,
где
- Вт/(м 2 ·К 4 ) — постоянная Стефана — Больцмана.
Таким образом, абсолютно чёрное тело при = 100 K излучает 5,67 ватта с квадратного метра поверхности. При 1000 K мощность излучения увеличивается до 56,7 киловатта с квадратного метра.
Для нечёрных тел приближённо , где — степень черноты. Для абсолютно чёрного тела , для других объектов в силу закона Кирхгофа степень черноты равна коэффициенту поглощения , где — коэффициент поглощения, — коэффициент отражения, а — коэффициент пропускания. Поэтому для уменьшения лучистого теплопереноса поверхность окрашивают в белый цвет или наносят блестящее покрытие, а для увеличения — затемняют.
Цветность чернотельного излучения

Цветность чернотельного излучения , или, вернее, цветовой тон излучения абсолютно чёрного тела при его определённой температуре, приведена в таблице:
| Температурный интервал в кельвинах | Цвет |
|---|---|
| до 1000 | Красный |
| 1000—2000 | Оранжевый |
| 2000—3000 | Жёлтый |
| 3000—4500 | Бледно-жёлтый |
| 4500—5500 | Желтовато-белый |
| 5500—6500 | Чисто белый |
| 6500—8000 | Голубовато-белый |
| 8000—15000 | Бело-голубой |
| 15000 и более | Голубой |
Цвета даны в сравнении с рассеянным дневным светом ( D 65 ). Реально воспринимаемый цвет может быть искажён адаптацией глаза к условиям освещения. Видимый цвет чёрных тел с разной температурой также представлен на диаграмме в начале статьи.
Термодинамика чернотельного излучения
В термодинамике равновесное тепловое излучение рассматривают как фотонный газ , состоящий из электронейтральных безмассовых частиц , заполняющий полость объёмом V в абсолютно чёрном теле ( ), с давлением P и температурой T , совпадающей с температурой стенок полости. Для фотонного газа справедливы следующие термодинамические соотношения :
| ( Термическое уравнение состояния ) |
| ( Калорическое уравнение состояния для внутренней энергии ) |
| ( Каноническое уравнение состояния для внутренней энергии) |
| (Каноническое уравнение состояния для энтальпии ) |
| (Каноническое уравнение состояния для потенциала Гельмгольца ) |
| (Каноническое уравнение состояния для потенциала Гиббса ) |
| (Каноническое уравнение состояния для потенциала Ландау ) |
| ( Химический потенциал ) |
| ( Энтропия ) |
| ( Теплоёмкость при постоянном объёме ) |
| ( Теплоёмкость при постоянном давлении ) |
| ( Показатель адиабаты ) |
| ( Уравнения адиабаты ) |
Для большей компактности в формулах использована радиационная постоянная a вместо постоянной Стефана — Больцмана σ :
| (Радиационная постоянная) |
где c — скорость света в вакууме .
Фотонный газ представляет собой систему с одной термодинамической степенью свободы .
Давление фотонного газа не зависит от объёма, поэтому для фотонного газа изотермический процесс ( T = const) является одновременно и изобарным процессом ( P = const) . С повышением температуры давление фотонного газа растёт очень быстро, достигая 1 атмосферы уже при T = 1,4⋅10 5 K , а при температуре 10 7 K (температура центра Солнца) давление достигает значения 2,5⋅10 7 атм (2,5⋅10 12 Па ) . Величина теплоёмкости излучения становится сравнимой с величиной теплоёмкости одноатомного идеального газа лишь при температурах порядка миллионов кельвинов.
Представление о температуре излучения было введено Б. Б. Голицыным (1893).
См. также
- Точка Дрейпера
- Фундаментальные физические постоянные
- Тепловое излучение
- Закон смещения Вина
- Vantablack
- Серое тело
Примечания
- Абсолютно чёрное тело // Большой энциклопедический политехнический словарь. — 2004.
- М. А. Ельяшевич . Абсолютно чёрное тело // Физическая энциклопедия. В 5 томах / Главный редактор А. М. Прохоров. — М. : Советская энциклопедия, 1988.
- ↑ Абсолютно чёрное тело // Физический энциклопедический словарь / Главный редактор А. М. Прохоров. — М. : Советская энциклопедия, 1983.
- Кочаров Г. Е. // Физическая энциклопедия / Гл. ред. А. М. Прохоров . — М. : Большая Российская энциклопедия , 1994. — Т. 4. — С. 594. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8 .
- . fn.bmstu.ru. Дата обращения: 28 сентября 2015. 28 сентября 2015 года.
- , с. 164—167.
- , с. 465—467.
- .
- , с. 157, 177, 349.
- , с. 59.
Литература
- Алмалиев А. Н., Копытин И. В., Корнев А. С., Чуракова Т. А. Термодинамика и статистическая физика: Статистика идеального газа. — Воронеж: Ворон. гос. ун-т, 2004. — 79 с.
- Базаров И. П. Термодинамика. — 5-е изд. — СПб. — М. — Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3 .
- Гуггенгейм. Современная термодинамика, изложенная по методу У. Гиббса / Пер. под ред. проф. С. А. Щукарева. — Л. — М.: Госхимиздат, 1941. — 188 с.
- Новиков И. И. Термодинамика. — М. : Машиностроение, 1984. — 592 с.
- Сычёв В. В. Сложные термодинамические системы. — 5-е изд., перераб. и доп.. — М. : Издательский дом МЭИ, 2009. — 296 с. — ISBN 978-5-383-00418-0 .
- Мартинсон Л. К., Смирнов Е. В. // Физика в техническом университете, 5-й том. — МГТУ им. Н. Э. Баумана.
Ссылки
- (flash-приложение)
- Keesey, Lori J. . NASA (12 декабря 2010).
- 2021-02-25
- 2