Норман Джулиус Забуски ( англ. Norman Julius Zabusky ; 4 января 1929 , Нью-Йорк — 5 февраля 2018 , Беэр-Шева ) — американский физик-теоретик и математик , автор работ по нелинейной физике , вычислительной гидродинамике и экспериментальной математике , наиболее известный по совместному с Мартином Крускалом открытию солитонов в уравнении Кортевега — де Фриза .

Биография

Норман Забуски родился в 1929 году в Бруклине в семье Хаймана и Анны Забуски. После окончания Бруклинской технической школы ( англ. Brooklyn Technical High School ) он поступил в Городской колледж Нью-Йорка , где в 1951 году получил степень бакалавра по электротехнике. Два года спустя он получил степень магистра по электротехнике в Массачусетском технологическом институте , а в 1959 году — докторскую степень по теоретической физике, защитив в Калифорнийском технологическом институте диссертацию на тему «Гидромагнитная устойчивость цилиндрических потоков плазмы» ( англ. Hydromagnetic stability of a streaming cylindrical plasma , научные руководители — и Леверетт Дейвис мл.). Следующий год Забуски провёл в качестве постдока в Институте физики Общества Макса Планка в Мюнхене, а затем стал исследователем в Лаборатории физики плазмы Принстонского университета . Уже в 1961 году он перешёл в Лаборатории Белла , где в 1968 году возглавил первый отдел вычислительных исследований. В 1976—1988 годах учёный занимал пост профессора математики в Питтсбургском университете , после чего перебрался в Ратгерский университет , где работал сначала профессором вычислительной гидродинамики ( англ. State of New Jersey Professor of Computational Fluid Dynamics ), а в 2000—2005 годах — профессором прикладной физики ( англ. Donald H. Jacobs Chair in Applied Physics ). Кроме того, в начале 1990-х годов в университете Забуски основал и руководил Лабораторией визиометрики и моделирования ( англ. Laboratory for Visiometrics and Modeling ). После выхода в отставку он был приглашённым исследователем в Институте Вейцмана в Израиле .

Забуски активно занимался правозащитной деятельностью. С 1981 года он был членом и в течение ряда лет состоял в его консультативном совете. В 1970-е — 1980-е годы учёный выступал в защиту советских «отказников» , во время визита в СССР в 1983 году встречался с рядом лишённых работы и права выезда физиков, из-за чего по распоряжению властей был выслан из страны .

Забуски скончался 5 февраля 2018 года от идиопатического лёгочного фиброза .

Научная деятельность

Забуски принадлежит ряд важных результатов в нелинейной физике , вычислительной гидродинамике , экспериментальной математике . В первой половине 1950-х годов он участвовал в прикладных исследованиях, связанных с военными разработками, — занимался расчётами системы обратной связи для управления движением торпед и моделированием динамики полёта управляемых ракет типа «Спэрроу» . Во второй половине 1950-х годов областью его исследований стала физика плазмы , в частности вопросы устойчивости потоков замагниченной плазмы, актуальные для решения проблем управляемого термоядерного синтеза . Выбор данного направления исследований вывел учёного на более общие и фундаментальные задачи, связанные с решением нелинейных уравнений .

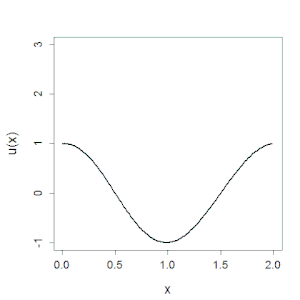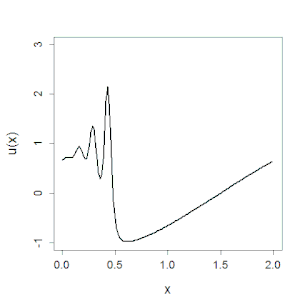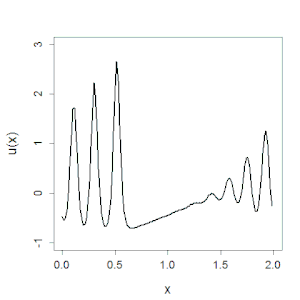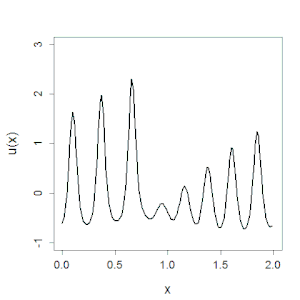
В 1965 году вместе с Мартином Крускалом Забуски обнаружил устойчивое локализованное решение нелинейного уравнения Кортевега — де Фриза (КдФ) , которое описывает длинные волны на мелководье и которое они получили в при рассмотрении известной . Хотя импульсные решения этого уравнения были известны и ранее, численные расчёты позволили выявить их новые неожиданные свойства. Оказалось, что эти импульсы ведут себя подобно частицам, не разрушаясь при прохождении друг через друга, а начальные возбуждения в системе распадаются на серию таких импульсов. Такие решения, которые Забуски и Крускал назвали солитонами , стали первым примером такого рода нелинейных волн , встречающихся в различных физических, химических, биологических системах. Их обнаружение оказалось мощным стимулом для развития нелинейной динамики, в частности для разработки в течение следующих нескольких лет метода обратной задачи рассеяния .

Во второй половине 1960-х годов Забуски совместно с Гэри Димом ( англ. Gary Deem ) численно исследовал солитонные решения так называемого модифицированного уравнения КдФ и поведение нелинейной цепочки в проблеме ФПУ с изменёнными начальными условиями, обнаружив новые её состояния (так называемые n-curve states , разновидность дискретного ). Вместе с Крускалом он исследовал законы сохранения для уравнения КдФ, нашёл несколько новых его инвариантов и доказал их единственность . В 1971 году Забуски и Гэлвин провели первое успешное сравнение результатов численного решения уравнения КдФ с экспериментальными измерениями волн на воде. С конца 1960-х годов научные интересы Забуски сместились в сторону вычислительной гидродинамики, в частности моделирования турбулентных потоков. Так, он показал необходимость учёта вихревых процессов для объяснения экспериментальных результатов, связанных с полётом баллистических ракет (1969, 1971); разработал алгоритм контурной динамики ( англ. contour dynamics ) для двумерного уравнения Эйлера (1973) и обобщил этот метод на случай ионизированной плазмы в ионосфере (1980); ввёл представление о так называемых V-состояниях, представляющих собой поступательно движущийся и вращающийся неизменный одиночный вихрь (1978) и т.д.

В ходе работы по численному решению нелинейных уравнений Забуски пришёл к выводу о важности визуализации получаемых решений. В 1990 году вместе с Франсуа Битцем ( François Bitz ) он предложил термин «визиометрика» ( англ. visiometrics ) для обозначения основанного на визуализации подхода к анализу свойств динамических и волновых систем и в дальнейшем активно популяризировал данное направление исследований .

Награды

• Стипендия Гуггенхайма (1971)
• Медаль Говарда Поттса (1986) «за работу в области математической физики и творческое сочетание анализа и вычислений, а также за работу по свойствам солитонов»
• Премия Отто Лапорте (2003) «за новаторский и продолжительный вклад в нелинейную и вихревую физику и вычислительную гидродинамику, в том числе: за солитон; контурную динамику и V-состояния для двумерных потоков; вихревые снаряды для ускоренных неоднородных потоков; и визиометрику для облегчения моделирования»

Избранные публикации

• Zabusky N.J., Kruskal M.D. Interaction of "Solitons" in a Collisionless Plasma and the Recurrence of Initial States // Physical Review Letters . — 1965. — Vol. 15, № 6 . — P. 240-243. — doi : .
• Zabusky N.J. A Synergetic Approach to Problems of Nonlinear Dispersive Wave Propagation and Interaction // Nonlinear Partial Differential Equations: A Symposium on Methods of Solution. — Academic Press , 1967. — P. 223-258. — doi : .
• Zabusky N.J. Solitons and Bound States of the Time-Independent Schrödinger Equation // Physical Review . — 1968. — Vol. 168, № 1 . — P. 124-128. — doi : .
• Zabusky N.J., Galvin C.G. Shallow-water waves, the Korteweg-deVries equation and solitons // Journal of Fluid Mechanics. — 1971. — Vol. 47, № 4 . — P. 811-824. — doi : .
• Tappert F.D., Zabusky N.J. Gradient-Induced Fission of Solitons // Physical Review Letters. — 1971. — Vol. 27, № 26 . — P. 1774-1776. — doi : .
• Deem G.S., Zabusky N.J. Vortex Waves: Stationary "V States," Interactions, Recurrence, and Breaking // Physical Review Letters. — 1978. — Vol. 40, № 13 . — P. 859-862. — doi : .
• Zabusky N.J., Hughes M.H., Roberts K.V. Contour dynamics for the Euler equations in two dimensions // Journal of Computational Physics. — 1979. — Vol. 30, № 1 . — P. 96-106. — doi : .
• Zabusky N.J. Computational synergetics and mathematical innovation // Journal of Computational Physics. — 1981. — Vol. 43, № 2 . — P. 195-249. — doi : .
• Overman E.A., Zabusky N.J. Evolution and merger of isolated vortex structures // The Physics of Fluids. — 1982. — Vol. 25, № 8 . — P. 1297-1305. — doi : .
• Melander M.V., Zabusky N.J., Mcwilliams J.C. // Journal of Fluid Mechanics. — 1988. — Vol. 195. — P. 303-340. — doi : .
• Samtaney R., Silver D., Zabusky N., Cao J. Visualizing features and tracking their evolution // Computer. — 1994. — Vol. 27, № 7 . — P. 20-27. — doi : .
• Zabusky N.J. Vortex paradigm for accelerated inhomogeneous flows: Visiometrics for the Rayleigh-Taylor and Richtmyer-Meshkov environments // Annual Review of Fluid Mechanics. — Annual Reviews , 1999. — Vol. 31. — P. 495-536. — doi : .

Примечания

Литература

• Campbell D.K., Newell A.C., Porter M.A. Norman Julius Zabusky // Physics Today . — 2018. — Vol. 71, № 8 . — P. 61. — doi : .
• Zabusky N.J. Fermi–Pasta–Ulam, solitons and the fabric of nonlinear and computational science: History, synergetics, and visiometrics // Chaos. — 2005. — Vol. 15, № 1 . — P. 015102 (16 pp). — doi : .

Ссылки

• Campbell D.K., Newell A.C., Porter M.A. // The Dynamical Systems Web. — Society for Industrial and Applied Mathematics. — Дата обращения: 11.09.2018.