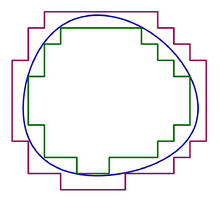
Мера Жордана — один из способов формализации понятия длины , площади и ${\displaystyle n}$ -мерного объёма в ${\displaystyle n}$ -мерном евклидовом пространстве .

Определение

Меру Жордана можно определить как единственную конечно-аддитивную меру , определённую на кольце многогранников и удовлетворяющую следующим условиям:

1. Меры конгруэнтных многогранников равны.
2. Мера единичного куба равна единице.

Максимальное кольцо множеств, на которое мера Жордана продолжается единственным образом, называется кольцом квадрируемых множеств .

Построение

Мера Жордана ${\displaystyle m\Delta }$ параллелепипеда ${\displaystyle \Delta =\prod _{i=1}^{n}[a_{i},\;b_{i}]}$ в ${\displaystyle \mathbb {R} ^{n}}$ определяется как произведение

${\displaystyle m\Delta =\prod _{i=1}^{n}(b_{i}-a_{i}).}$

Для ограниченного множества ${\displaystyle E\subset \mathbb {R} ^{n}}$ определяются:

• внешняя мера Жордана

  ${\displaystyle m_{e}E=\inf \sum _{k=1}^{N}m\Delta _{k},\quad \bigcup _{k}\Delta _{k}\supset E}$

• внутренняя мера Жордана

  ${\displaystyle m_{i}E=\sup \sum _{k=1}^{N}m\Delta _{k},\quad \bigcup _{k}\Delta _{k}\subset E,\quad \Delta _{k}\cap \Delta _{m}=\varnothing }$ , если ${\displaystyle k\neq m,}$

здесь ${\displaystyle \Delta _{1},\;\Delta _{2},\;\ldots ,\;\Delta _{N}}$ — параллелепипеды описанного выше вида.

Множество ${\displaystyle E}$ называется измеримым по Жордану (или квадрируемым ), если ${\displaystyle m_{e}E=m_{i}E}$ . В этом случае мера Жордана равна ${\displaystyle mE=m_{e}E=m_{i}E}$ .

Свойства

• Множества, измеримые по Жордану, образуют кольцо , на котором мера Жордана является конечно-аддитивной мерой .
• Мера Жордана инвариантна относительно движений евклидова пространства.
• Множество ${\displaystyle F}$ измеримо по Жордану, если для любого ${\displaystyle \varepsilon >0}$ существует пара многогранников ${\displaystyle P}$ и ${\displaystyle Q}$ таких, что

  ${\displaystyle P\subset F\subset Q}$ и ${\displaystyle mP+\varepsilon >mQ}$ .

• Ограниченное множество ${\displaystyle E\subset \mathbb {R} ^{n}}$ измеримо по Жордану тогда и только тогда, когда его граница имеет нулевую меру Жордана (или, что равносильно, когда его граница имеет нулевую меру Лебега ). В частности, все множества, граница которых состоит из конечного числа гладких кривых и точек, измеримы по Жордану. Тем не менее существуют множества, ограниченные простой замкнутой кривой Жордана , которые не измеримы по Жордану.
• Внешняя мера Жордана одна и та же для ${\displaystyle E}$ и ${\displaystyle {\bar {E}}}$ (замыкания множества ${\displaystyle E}$ ) и равна мере Бореля ${\displaystyle {\bar {E}}}$ .

История

Приведённое понятие меры ввели Пеано ( 1887 ) и Жордан ( 1892 ). Впоследствии понятие было обобщено Лебегом на более широкий класс множеств.

Пример множества, неизмеримого по Жордану

Рассмотрим меру Жордана ${\displaystyle m}$ , определённую на ${\displaystyle \mathbb {R} }$ . Пусть ${\displaystyle A=\left[0,1\right]=\{x\in \mathbb {R} \colon 0\leqslant x\leqslant 1\}}$ — множество точек единичного отрезка., ${\displaystyle \mathbb {Q} }$ — подмножество рациональных точек множества ${\displaystyle A}$ , тогда ${\displaystyle \mathbb {Q} }$ — неизмеримое по Жордану множество, так как ${\displaystyle m_{e}\mathbb {Q} =1,\;m_{i}\mathbb {Q} =0,\;m_{e}\mathbb {Q} \neq m_{i}\mathbb {Q} }$ , то есть верхняя и нижняя мера Жордана не совпадают (хотя это множество измеримо по Лебегу ).

Литература

• Колмогоров А.Н. , Фомин С.В. Элементы теории функций и функционального анализа. — изд. четвёртое, переработанное. — М. : Наука , 1976 . — 544 с.
• Кудрявцев Л.Д., Кутасов А.Д. Сборник задач по математическому анализу, глава 3;
• Peano, G. Applicazioni geometriche del calcolo infinitesimale. — Torino, 1887;
• Jordan, C. Journal de Mathématiques Pures et Appliquées. — 1892. — t. 8. — p. 69—99;

См. также

• Мера множества
• Мера Лебега
• Мера Хаусдорфа
• Мера Бореля