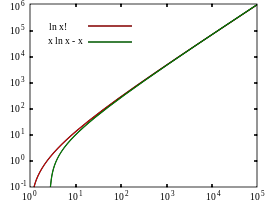
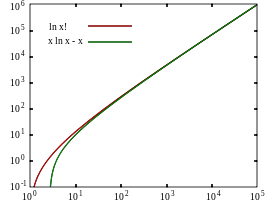
Отношение (ln
n
!) к (
n
ln
n
−
n
) стремится к 1 с увеличением
n
В математике
формула Стирлинга
(также
формула Муавра — Стирлинга
) — формула для
приближённого вычисления
факториала
и
гамма-функции
. Названа в честь
Джеймса Стирлинга
и
Абрахама де Муавра
, последний считается автором формулы
.
Наиболее используемый вариант формулы:
ln
Γ
(
n
+
1
)
=
ln
n
!
=
n
ln
n
−
n
+
O
(
ln
n
)
.
{\displaystyle \ln \Gamma (n+1)=\ln n!=n\ln n-n+O(\ln n).}
Следующий член в
O
(
ln
n
)
{\displaystyle O(\ln n)}
это
1
2
ln
(
2
π
n
)
{\displaystyle {\frac {1}{2}}\ln(2\pi n)}
; таким образом более точная аппроксимация:
lim
n
→
∞
n
!
2
π
n
(
n
e
)
n
=
1
,
{\displaystyle \lim _{n\to \infty }{\frac {n!}{{\sqrt {2\pi n}}\,\left({\frac {n}{e}}\right)^{n}}}=1,}
что эквивалентно
n
!
∼
2
π
n
(
n
e
)
n
.
{\displaystyle n!\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}.}
Часто формулу Стирлинга записывают в виде
n
!
=
2
π
n
(
n
e
)
n
exp
θ
n
12
n
,
{\displaystyle n!={\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\exp {\frac {\theta _{n}}{12n}},}
где
0
<
θ
n
<
1
{\displaystyle 0<\theta _{n}<1}
,
n
>
0
{\displaystyle n>0}
.
Более точную оценку даёт формула
n
!
=
2
π
n
(
n
e
)
n
exp
1
12
n
+
θ
n
,
{\displaystyle n!={\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\exp {\frac {1}{12n+\theta _{n}}},}
где
0
<
θ
n
<
1
{\displaystyle 0<\theta _{n}<1}
,
n
>
0
{\displaystyle n>0}
.
В последней формуле максимальное значение
θ
n
{\displaystyle \theta _{n}}
в действительности меньше 1 и примерно равно 0,7509.
Формула Стирлинга является приближением, полученным из разложения факториала в
ряд Стирлинга
, который при
n
>
0
{\displaystyle n>0}
имеет вид
n
!
∼
2
π
n
(
n
e
)
n
exp
∑
k
=
1
∞
B
2
k
2
k
(
2
k
−
1
)
n
2
k
−
1
=
=
2
π
n
(
n
e
)
n
(
1
+
1
12
n
+
1
288
n
2
−
139
51840
n
3
−
571
2488320
n
4
+
⋯
)
=
=
2
π
n
(
n
e
)
n
(
1
+
1
(
2
1
)
(
6
n
)
1
+
1
(
2
3
)
(
6
n
)
2
−
139
(
2
3
)
(
2
⋅
3
⋅
5
)
(
6
n
)
3
−
−
571
(
2
6
)
(
2
⋅
3
⋅
5
)
(
6
n
)
4
+
⋯
)
,
{\displaystyle {\begin{aligned}n!&\sim {\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\exp \sum _{k=1}^{\infty }{\frac {B_{2k}}{2k(2k-1)n^{2k-1}}}=\\&={\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\left(1+{\frac {1}{12n}}+{\frac {1}{288n^{2}}}-{\frac {139}{51840n^{3}}}-{\frac {571}{2488320n^{4}}}+\cdots \right)=\\&={\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}\left(1+{\frac {1}{(2^{1})(6n)^{1}}}+{\frac {1}{(2^{3})(6n)^{2}}}-{\frac {139}{(2^{3})(2\cdot 3\cdot 5)(6n)^{3}}}-{}\right.\\&\qquad \left.{}-{\frac {571}{(2^{6})(2\cdot 3\cdot 5)(6n)^{4}}}+\cdots \right),\end{aligned}}}
где
B
j
{\displaystyle B_{j}}
—
числа Бернулли
с номером
j
{\displaystyle j}
.
В этой формуле используется символ эквивалентности вместо равенства, так как
ряд расходится
при каждом фиксированном
n
{\displaystyle n}
, однако он является
асимптотическим разложением
факториала при
n
→
∞
{\displaystyle n\to \infty }
.
Ссылки
Pearson, Karl (1924), "Historical note on the origin of the normal curve of errors",
Biometrika
,
16
: 402–404 [p. 403],
doi
:
: «Стирлинг лишь показал, что арифметическая константа в формуле Муавра равна
2
π
{\displaystyle {\sqrt {2\pi }}}
. Я считаю, что это не делает его автором теоремы».
Ссылки на внешние ресурсы
Словари и энциклопедии