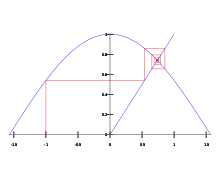
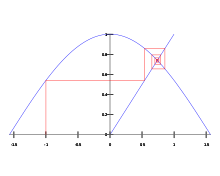
Число Дотти является единственной
неподвижной точкой
функции
косинуса
.
Число́ До́тти
—
постоянная
, определяемая как
вещественное
решение уравнения
cos
x
=
x
,
{\displaystyle \cos x=x,}
где аргумент
cos
{\displaystyle \cos }
измеряется в
радианах
. В
десятичном представлении
число Дотти примерно равно
0
,
739085133215...
{\displaystyle 0,739085133215...}
.
Из
теоремы о промежуточном значении
следует, что указанное уравнение должно иметь хотя бы одно решение.
Производная
функции
x
−
cos
(
x
)
{\displaystyle x-\cos(x)}
равна
sin
(
x
)
+
1
{\displaystyle \sin(x)+1}
и
почти везде
положительна, а значит, сама функция
монотонно возрастает
и не может иметь нескольких нулей. Таким образом, уравнение
cos
x
=
x
{\displaystyle \cos x=x}
однозначно определяет рассматриваемую константу.
Значения тригонометрических функций
Пусть
D
{\displaystyle D}
— число Дотти. Тогда:
s
i
n
(
D
)
≈
0
,
673612029183
{\displaystyle \mathrm {sin} (D)\approx 0,673612029183}
t
g
(
D
)
≈
0
,
911413312094
{\displaystyle \mathrm {tg} (D)\approx 0,911413312094}
Свойства
Число Дотти является нетривиальной
притягивающей неподвижной точкой
функции
косинуса
на сколь угодно большой своей
действительной
(но не
комплексной
)
окрестности
. Иначе говоря, для любого действительного
x
{\displaystyle x}
число
lim
n
→
∞
(
cos
(
cos
(
…
cos
(
x
)
…
)
)
⏟
n
)
{\displaystyle \lim \limits _{n\to \infty }(\underbrace {\cos(\cos(\dots \cos(x)\dots ))} _{n})}
равно константе Дотти. Уравнение
cos
z
=
z
{\displaystyle \cos z=z}
для
комплексного
z
{\displaystyle z}
имеет, кроме неё, бесконечное количество решений, однако ни одно из них не является
притягивающей неподвижной точкой
.
Кроме того, число Дотти
трансцендентно
, что можно доказать при помощи
теоремы Линдемана — Вейерштрасса
.
С использованием
теоремы Лагранжа об обращении рядов
было доказано, что число Дотти представимо в виде
ряда
π
2
+
∑
n
=
1
∞
a
2
n
−
1
π
2
n
−
1
{\displaystyle {\frac {\pi }{2}}+\sum _{n=1}^{\infty }a_{2n-1}\pi ^{2n-1}}
, где
a
n
{\displaystyle a_{n}}
для любого нечётного
n
{\displaystyle n}
является
рациональным
числом, определённым следующим образом:
a
n
=
1
n
!
2
n
lim
t
→
π
2
∂
n
−
1
∂
t
n
−
1
(
cos
t
t
−
π
/
2
−
1
)
−
n
{\displaystyle {\begin{aligned}a_{n}&={\frac {1}{n!\;2^{n}}}\lim _{t\to {\frac {\pi }{2}}}{\frac {\partial ^{n-1}}{\partial t^{n-1}}}{\left({\frac {\cos t}{t-\pi /2}}-1\right)^{-n}}\end{aligned}}}
Первые несколько членов последовательности
(
a
n
)
{\displaystyle (a_{n})}
равны
−
1
4
,
−
1
768
,
−
1
61440
,
−
43
165150720
,
…
{\displaystyle -{\frac {1}{4}},-{\frac {1}{768}},-{\frac {1}{61440}},-{\frac {43}{165150720}},\ldots }
Формула в Excel
Формула для числа Дотти в Excel или LibreOffice Calc:
SQRT(1-(2*BETA.INV(1/2;1/2;3/2)-1)^2)
.
Происхождение названия
Имя данной константе было дано Самюэлем Капланом в честь преподавательницы французского по имени Дотти, которая обнаружила её, нажимая раз за разом кнопку взятия косинуса на калькуляторе, и рассказала об этом своему мужу — учителю математики.
Сноски
Примечания
(неопр.)
.
oeis.org
.
Дата обращения: 26 мая 2019.
26 мая 2019 года.
Eric W. Weisstein.
(неопр.)
.
Дата обращения: 24 апреля 2020.
18 марта 2020 года.
↑
Kaplan, Samuel R.
(англ.)
//
Mathematics Magazine
: magazine. — 2007. — February (
vol. 80
). —
P. 73
.
12 ноября 2020 года.
(неопр.)
oeis.org
.
Дата обращения: 26 мая 2019.
26 мая 2019 года.
(неопр.)
.
oeis.org
.
Дата обращения: 22 июля 2019.
22 июля 2019 года.
Ссылки
Т. Миллер (1890)
Валерий Салов (2012)
Mohammad K. Azarian (2008)