Interested Article - Модель Бертрана
- 2020-01-10
- 2
Модель Бертрана или конкуренция по Бертрану — модель ценовой конкуренции на олигополистическом рынке , сформулированная французским математиком и экономистом Жозефом Бертраном в 1883 году.
Модель описывает поведение фирм на олигополистическом рынке , конкурирующих за счет изменения уровня цен на свою продукцию. Парадоксальный вывод модели — фирмы будут назначать цену, равную предельным издержкам , как и фирмы в условиях совершенной конкуренции — назван парадоксом Бертрана .
Предположения модели
В модели приняты следующие предположения:
- На рынке имеется по меньшей мере две фирмы, производящие однородный продукт;
- Фирмы ведут себя некооперативно;
- Предельные издержки ( MC ) фирм одинаковы и постоянны;
- Функция спроса линейна;
- Фирмы конкурируют, устанавливая цену на свою продукцию, и выбирают её независимо и одновременно;
- После выбора цены фирмы производят объем товара, равный величине спроса на их продукцию;
- Если цены различны, потребители предъявляют спрос на более дешевый товар;
- Если цены одинаковы, приобретаются товары всех фирм в равных долях.
- Модель статична (рассматривается принятие решения в единичный момент времени).
Предположение о ценовой конкуренции означает, что фирмы могут легко изменять объем выпуска продукции, однако изменить цену после выбора очень трудно или невозможно.
Равновесие в классической модели Бертрана
- MC = предельные издержки
- p 1 = цена фирмы 1
- p 2 = цена фирмы 2
- p M = монопольная цена
Оптимальная цена фирмы 1 зависит от её ожиданий относительно цены, назначаемой фирмой 2. Назначение своей цены немного ниже цены конкурента позволяет получить весь спрос потребителей D и максимизирует прибыль. Если фирма 1 ожидает, что фирма 2 будет устанавливать цену, не превышающую предельных издержек MC , то её является установление цены, равной предельным издержкам.
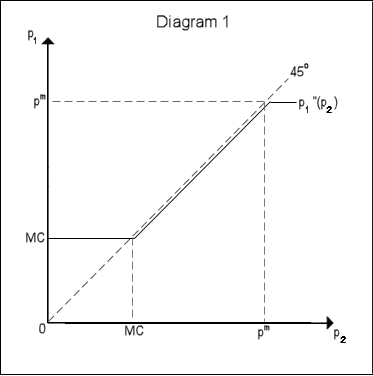
На диаграмме 1 показана функция наилучших ответов фирмы 1 p 1 ’’( p 2 ). Она показывает, что при p 2 < MC фирма 1 устанавливает p 1 = MC . При p 2 в интервале между MC и монопольной ценой p M фирма 1 назначает цену немного меньше p 2 . Наконец, если p 2 выше p M , фирма 1 назначает монопольную цену p 1 =p M .

Так как функции издержек обеих фирм одинаковы, наилучший ответ фирмы 2 p 2 ’’( p 1 ) будет симметричным относительно диагонали I координатного угла. Функции наилучших ответов обеих фирм приведены на диаграмме 2.

Результатом выбора стратегий фирмами является равновесие Нэша , представляющее собой пару цен ( p 1 , p 2 ) от которых невыгодно отклоняться ни одной фирме. Оно может быть найдено как точка пересечения кривых наилучших ответов (точка N на диаграмме). Видно, что в этой точке p 1 = p 2 = MC , т.е. обе фирмы устанавливают свои цены равными предельным издержкам.
Выводы
Модель Бертрана имеет два разумных исхода:
- кооперативный, подразумевающий достижение фирмами соглашения, при котором они взимают монопольную цену и обслуживают каждый по половине спроса потребителей;
- конкурентный, при котором фирмы действуют некооперативно и устанавливают цену на уровне предельных издержек.
В несимметричном случае, когда одна из фирм имеет более низкие предельные издержки (например, при использовании лучшей технологии производства), она может устанавливать цену ниже предельных издержек конкурента и получить весь рынок. Это явление получило название .
См. также
Литература
- Bertrand, J. Book review of theorie mathematique de la richesse sociale and of recherches sur les principles mathematiques de la theorie des richesses // Journal de Savants. - 1883. - v.67. - P. 499–508.
- 2020-01-10
- 2