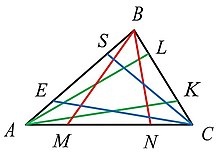
Недианы (или n-дианы) треугольника (англ. nedian или n-dian) — чевианы , соединяющие вершину треугольника и точки противолежащей стороны, которые отстоят на ${\displaystyle {\frac {1}{n}}}$ длины от её концов.

Чисто n конкретизирует название недиан, например, при n = 2 мы получим середины сторон, а недианы станут медианами , при n = 3 — тридианами, при n = 4 — тетрадианами, при n = 5 — пентадианами и т.д.

При n > 2 недианы треугольника разделяют на передние и задние . К передним недианам относят: BM, AK и CS, задними считают BN, AL и CE (См. рисунок 1).

Кроме того, все недианы треугольника можно разделить на две группы: нижние и верхние.

Верхними недианами будем называть те, что расположены ближе к вершине треугольника, например, AL и CS при вершине B. Тогда нижними будут недианы AK и CN (См. рисунок 1). Недианы, выходящие из одной вершины будем называть смежными (например, BM и BN) .

Недианов треугольник

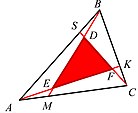
При попарном пересечении передних (или задних) недиан образуется недианов треугольник DEF (См. рисунок 2). В общем случае отношение площади недианова треугольника к площади исходного треугольника выражается соотношением: ${\displaystyle {\frac {S_{\Delta {DEF}}}{S_{\Delta {ABC}}}}={\frac {(n-2)^{2}}{n^{2}-n+1}}}$ . Данное соотношение является частным случаем теоремы Рауса .

При n = 3 площадь недианова треугольника составляет 1/7 от площади исходного треугольника ABC и является решением известной Ричарда Фейнмана , которую в своё время решали различными способами Мартин Гарднер , Роберт Потс и другие.

Недианов шестиугольник

При попарном пересечении всех 6-ти недиан треугольника образуется недианов шестиугольник FGHIJK (См. рисунок 3). Отношение площади полученного шестиугольника к площади исходного треугольника: ${\displaystyle {\frac {S_{FGHIJK}}{S_{\Delta {ABC}}}}={\frac {2(n-2)^{2}}{(n+1)(2n-1)}}}$

Примечания