Interested Article - Центральная прямая

amity
  • 2021-11-17
  • 1

Центральные прямые — это некоторые специальные прямые , связанные с треугольником и лежащие в плоскости треугольника. Особое свойство, которое отличает прямые как центральные прямые , проявляется через уравнение прямой в трилинейных координатах . Это особое свойство также связано с понятием . Понятие центральной прямой было введено Кларком Кимберлингом в статье, опубликованной в 1994 году .

Определение

Пусть ABC — треугольник, и пусть ( x : y : z ) — трилинейные координаты произвольной точки в плоскости треугольника ABC . Прямая линия в плоскости треугольника ABC будет центральной прямой треугольника ABC , если её уравнение в трилинейных координатах имеет вид

f ( a , b , c ) x + g ( a , b , c ) y + h ( a , b , c ) z = 0

где точка с трилинейными координатами ( f ( a , b , c ) : g ( a , b , c ) : h ( a , b , c )) является центром плоского треугольника ABC.

Центральные прямые как трилинейные поляры

Геометрически связь между центральной прямой и связанным с ней центром может быть выражена с использованием термина трилинейной поляры и изогонального сопряжения . Пусть X = ( u ( a , b , c ) : v ( a , b , c ) : w ( a , b , c )) — центр треугольника. Тогда уравнение трилинейной поляры треугольного центра X есть

x / u ( a , b , c ) + y / v ( a , b , c ) y + z / w ( a , b , c ) = 0.

Аналогично Y = (1 / u ( a , b , c ) : 1 / v ( a , b , c ) : 1 / w ( a , b , c )) является изогональным сопряжением центра X .

Таким образом, центральная прямая, описываемая уравнением

f ( a , b , c ) x + g ( a , b , c ) y + h ( a , b , c ) z = 0,

является трилинейной полярой при изогональном сопряжении центра ( f ( a , b , c ) : g ( a , b , c ) : h ( a , b , c )).

Построение центральных прямых

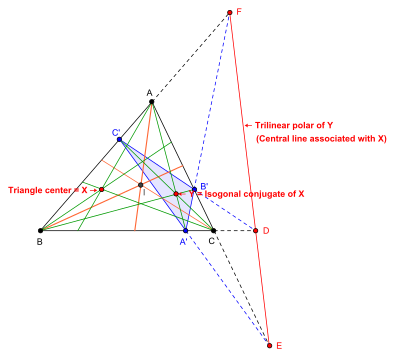
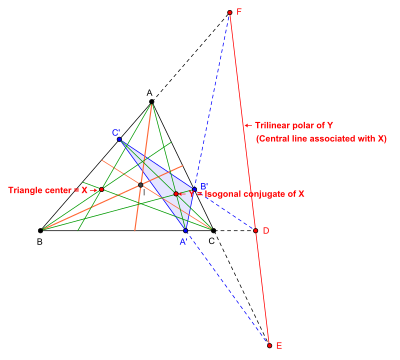
Пусть X — любой центр треугольника ABC .

  • Проведём прямые AX , BX и CX и построим их отражения относительно биссектрис углов треугольника при вершинах соответственно A , B , C .
  • Отражённые прямые пересекутся, и точка их пересечения будет изогональным сопряжением Y точки X .
  • Пусть чевианы AY , BY , CY пересекают противоположные стороны треугольника ABC в точках A' , B' , C' . Тогда треугольник A’B’C' является чевианным треугольником точки Y .
  • Треугольник ABC и чевианный треугольник A’B’C' находятся в перспективе, и пусть прямая DEF — ось перспективности двух треугольников. Прямая DEF — трилинейная поляра точки Y . Прямая DEF — центральная прямая, связанная с центром X .

Некоторые именные центральные прямые

Пусть X n — n -й центр треугольника в энциклопедии центров треугольника Кларка Кимберлинга. Центральная прямая, связанная с X n обозначается как L n . Некоторые именные центральные линии даются ниже.

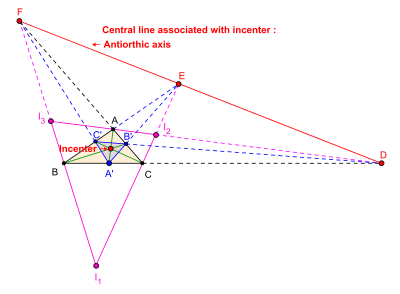
Антиортовая ось (Antiorthic axis) как ось перспективности треугольника ABC и его треугольника трех центров вневписанных окружностей ( треугольник трёх внешних биссектрис )

Центральная прямая, связанная с X 1 , то есть с центром вписанной окружности: антиортовая ось

Центральная прямая, связанная с инцентром X 1 = (1 : 1 : 1) (также обозначаемым как I ) даётся уравнением

x + y + z = 0.

Эта прямая является антиортовой осью треугольника ABC .

  • Изогонально сопряженный инцентру треугольника ABC центр — это сам инцентр . Таким образом, антиортовая ось, которая является центральной линией, связанной с инцентром , является осью перспективности треугольника ABC и чевианного треугольник инцентра треугольника ABC .
  • Антиортовая ось треугольника ABC является осью перспективности треугольника ABC и треугольника центров трёх вневписанных окружностей ( треугольник трёх внешних биссектрис ) I 1 I 2 I 3 треугольника ABC .
  • Треугольник, боковые стороны которого внешне касаются трёх центров вневписанных окружностей треугольника ABC является внешне тангенцальным треугольником ( the extangents triangle ) треугольника ABC . Треугольник ABC и его внешне тангенцальный треугольник находятся в перспективе, и ось их перспективности является антиортовой осью треугольника ABC .
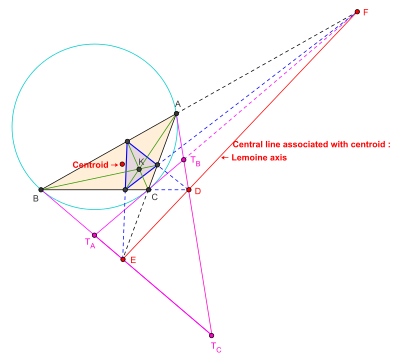
Ось Лемуана — трилинейная поляра точки Лемуана показана красным цветом

Центральная прямая, связанная с X 2 , то есть с центроидом : ось Лемуана

Трилинейное координаты центроида X 2 (также обозначается как G ) треугольника ABC есть (1 / a : 1 / b : 1 / c ). Таким образом, центральная прямая, связанная с центроидом (центром тяжести) в трилинейных координатах задаётся уравнением

x / a + y / b + z / c = 0.

Эта прямая является осью Лемуана треугольника ABC .

  • Изогонально сопряженная центроиду X 2 точка является точкой Лемуана X 6 (точка пересечения трёх симедиантреугольника) (также обозначается как K ), имеющая трилинейные координаты ( a : b : c ). Таким образом, ось Лемуана треугольника ABC является трилинейной полярой точки пересечения симедиан треугольника ABC .
  • Тангенциальный треугольник треугольника ABC является треугольник T A T B T C , образованный касательными к окружности треугольника ABC в его вершинах. Треугольник ABC и его тангенциальный треугольник находятся в перспективе, а их осью перспективности является ось Лемуана треугольника ABC .

Центральная прямая, связанная с X 3 , то есть с центром описанной окружности: Ось высот (Orthic axis)

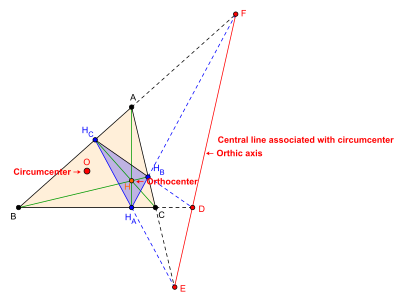
Трилинейные координаты центра описанной окружности X 3 (также обозначается как O ) треугольника ABC есть (cos A : cos B : cos C ). Таким образом, центральная прямая, связанная с центром описанной окружности в трилинейных координатах задаётся уравнением

x cos A + y cos B + z cos C = 0.

Эта прямая является осью высот треугольника ABC .

  • Изогональным сопряжением центра описанной окружности X 6 является ортоцентр X 4 (также обозначается как H ), имеющий трилинейные координаты (sec A : sec B : sec C ). Таким образом, ось высот треугольника ABC является трилинейной полярой ортоцентра для треугольника ABC . Ось высот треугольника ABC является осью перспективности треугольника ABC и его треугольника высот (orthic triangle) H A H B H C .

Центральная прямая, связанная с X 4 , то есть с ортоцентром

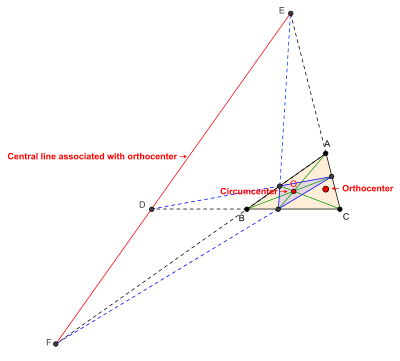
Центральная линия, связанная с центром описанной окружности

Трилинейные координаты ортоцентра X 4 ((также обозначается как H ) треугольника ABC есть(sec A : sec B : sec C ). Таким образом, центральная прямая, связанная с центром описанной окружности в трилинейных координатах задаётся уравнением

x sec A + y sec B + z sec C = 0.
  • Изогональным сопряжением ортоцентра треугольника является центр описанной окружности треугольника. Таким образом, центральная прямая, связанная с ортоцентром, является трилинейной полярой центра описанной окружности.

Центральная прямая, связанная с X 5 , то есть с центром окружности девяти точек

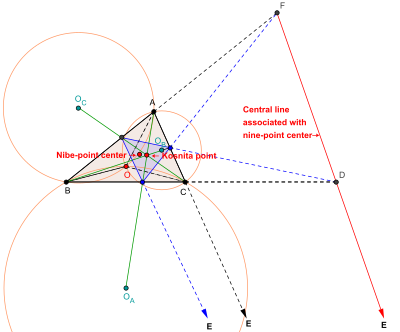
Трилинейные координаты центра окружности девяти точек X 5 (также обозначается как N ) треугольника ABC есть (cos ( B − C ) : cos ( C − A ) : cos ( A − B )). . Таким образом, центральная прямая, связанная с центром окружности девяти точек в трилинейных координатах задаётся уравнением

x cos ( B − C ) + y cos ( C − A ) + z cos ( A − B ) = 0.
  • Изогональное сопряжение центра окружности девяти точек треугольника ABC есть точка Коснита X 54 треугольника ABC . . Таким образом, центральная прямая, связанная с центром окружности девяти точек является трилинейной полярой для точки Коснита.
  • Точка Коснита строится следующим образом. Пусть O — центр описанной окружности треугольника ABC . Пусть O A , O B , O C — центры описанных окружностей соответственно треугольников BOC , COA , AOB .Прямые AO A , BO B , CO C пересекаются в одной точке, и точка их пересечения это — точка Коснита для треугольника ABC . Ее название связано J. Rigby.

Центральная прямая, связанная с X 6 , то есть с точкой пересечения симедиан: бесконечно удаленная прямая

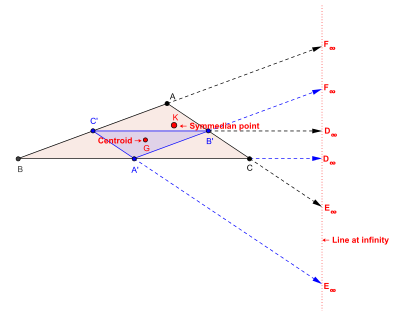
Трилинейные координаты точки пересечения трех симедиан ( Точка Лемуана ) X 6 (также обозначается как K ) треугольника ABC есть ( a : b : c ). Таким образом, центральная прямая, связанная с точкой пересечения трех симедиан в трилинейных координатах задаётся уравнением

a x + b y + c z =0.
  • Эта линия является бесконечно удаленной прямой в плоскости треугольника ABC .
  • Изогональное сопряжённой к точке пересечения симедиан треугольника ABC является центроидом треугольника ABC . Таким образом, центральная прямая, связанная с точкой пересечения симедиан, является трилинейной полярой центроида. Она является осью перспективности треугольника ABC и его дополнительного треугольника (он же — серединный треугольник = medial triangle).

Некоторые другие именные центральные прямые

Прямая Эйлера

Прямая Эйлера треугольника ABC является прямой, проходящей через центр тяжести, ортоцентр и центр описанной окружности треугольника ABC . Её уравнение в трилинейных координатах есть

x sin 2 A sin ( B − C ) + y sin 2 B sin ( C − A ) + z sin 2 C sin ( C − A ) = 0.

Это центральная прямая, связанная с точкой X 647 .

Ось Брокара

Ось Брокара треугольника ABC является прямой, проходящей через центр описанной окружности треугольника и точку пересечения трех симедиан треугольника ABC . Её уравнение в трилинейных координатах есть

x sin ( B — C ) + y sin ( C — A ) + z sin ( A — B ) = 0.

Эта центральная прямая связана с центром X 523 .

См. также

Примечания

  1. Kimberling, Clark. (англ.) // Mathematics Magazine : magazine. — 1994. — June ( vol. 67 , no. 3 ). — P. 163—187 . — doi : .
  2. ↑ Kimberling, Clark. (неопр.) . — Winnipeg, Canada: Utilitas Mathematica Publishing, Inc., 1998. — С. 285. 10 марта 2016 года.
  3. Weisstein, Eric W. . From MathWorld--A Wolfram Web Resource . Дата обращения: 24 июня 2012. 17 сентября 2012 года.
  4. Kimberling, Clark . Дата обращения: 24 июня 2012. 23 апреля 2012 года.
  5. Weisstein, Eric W. . From MathWorld--A Wolfram Web Resource. . Дата обращения: 28 июня 2012. 17 августа 2012 года.
  6. Weisstein, Eric W. . From MathWorld--A Wolfram Web Resource. . Дата обращения: 28 июня 2012. 18 августа 2012 года.
  7. Weisstein, Eric W. . From MathWorld--A Wolfram Web Resource . Дата обращения: 26 июня 2012. 18 августа 2012 года.
  8. Weisstein, Eric W. . From MathWorld--A Wolfram Web Resource. . Дата обращения: 19 апреля 2016. 29 апреля 2016 года.
  9. Weisstein, Eric W. . From MathWorld--A Wolfram Web Resource. . Дата обращения: 29 июня 2012. 6 мая 2012 года.
  10. Weisstein, Eric W. . From MathWorld--A Wolfram Web Resource . Дата обращения: 29 июня 2012. 6 мая 2012 года.
  11. Darij Grinberg. (англ.) // (англ.) ( : journal. — 2003. — Vol. 3 . — P. 105—111 . 4 марта 2016 года.
  12. J. Rigby. Brief notes on some forgotten geometrical theorems (неопр.) // Mathematics & Informatics Quarterly. — 1997. — Т. 7 . — С. 156—158 .
Источник —

amity
  • 2021-11-17
  • 1
  • Tags:

Same as Центральная прямая

The title for the last searches