Interested Article - Точки Вектена

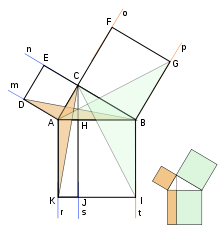
В планиметрии внешняя и внутренняя точки Вектена — точки, которые строятся на основе данного треугольника аналогично первой и второй точкам Наполеона . Однако для построения выбираются центры не равносторонних треугольников, а квадратов, построенных на сторонах данного треугольника (см. рис.).

Внешняя точка Вектена

Пусть ABC — произвольный треугольник . На его сторонах BC, CA, AB наружу построим три квадрата соответственно с центрами $O_{a},O_{b},O_{c}$ . Тогда линии $AO_{a},BO_{b}$ и $CO_{c}$ пересекаются в одной точке, называемой внешней точкой Вектена треугольника ABC.

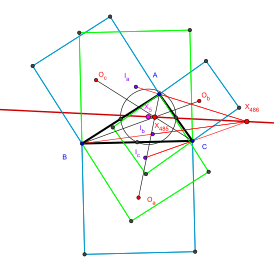
В Энциклопедии центров треугольника внешняя точка Вектена обозначается как X(485) .

История

Внешняя точка Вектена названа так в начале 19-го века в честь французского математика Вектена, который изучал математику в одно время с Жергонном (Joseph Diaz Gergonne) в Ниме (Nîmes) и опубликовал своё исследование о фигуре в виде трех квадратов, построенной на трех сторонах треугольника в 1817-ом году . По другим данным, это произошло в 1812/1813 годах. При этом ссылаются на работу .

Внутренняя точка Вектена

Пусть ABC — произвольный треугольник . На его сторонах BC, CA, AB вовнутрь построим три квадрата соответственно с центрами $I_{a},I_{b},I_{c}$ . Тогда линии $AI_{a},BI_{b}$ и $CI_{c}$ пересекаются в одной точке, называемой внутренней точкой Вектена треугольника ABC. В Энциклопедии центров треугольника внутренняя точка Вектена обозначается как X(486) .

Прямая $X(485)X(486)$ пересекает прямую Эйлера в Центре девяти точек треугольника $ABC$ . Точки Вектена лежат на гиперболе Киперта .

Положение на гиперболе Киперта

Координаты внешней и внутренней точек Вектена получаются из уравнения гиперболы Киперта при значениях угла $\theta$ при основаниях треугольников соответственно π/4 и -π/4.

Ассоциации

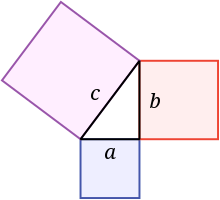
Рисунок выше для построения внешней точки Вектена в случае, если оно проводится для прямоугольного треугольника совпадает с рисунком одного из доказательств теоремы Пифагора (см. на рис. ниже так называемые пифагоровы штаны ).

*Пифагоровы штаны* . Сумма площадей квадратов, опирающихся на катеты $a$ и $b$ , равна площади квадрата, построенного на гипотенузе $c$

*Пифагоровы штаны* . Чертёж к доказательству Евклида. Основное направление доказательства — установление конгруэнтности $\triangle ACK\cong \triangle ABD$ , площадь которых составляет половину площади прямоугольников $AHJK$ и $ACED$ соответственно.

См. также

Точки Наполеона — пара треугольных центров, построенных аналогичным образом с использованием равносторонних треугольников вместо квадратов

Примечания

↑ Kimberling, Clark . Дата обращения: 15 января 2016. 19 апреля 2012 года.
Ayme, Jean-Louis, (PDF) , Дата обращения: 4 ноября 2014 от 5 марта 2016 на Wayback Machine
, , . Discrete Optimization II. — Amsterdam: Elsevier , 2000. — ISBN 978-0-08-086767-0 .