Interested Article - Теорема Микеля

- 2020-05-28
- 1
Теорема Микеля — утверждение в планиметрии, связанное с пересечением трёх окружностей, построенных вокруг вершин треугольника. Названа в честь французского математика . Эта теорема — один из нескольких результатов, касающийся окружностей в геометрии , полученный Микеле и опубликованных им в Journal de mathématiques pures et appliquées .
Формулировка
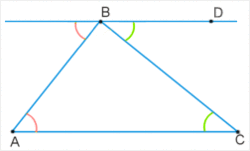
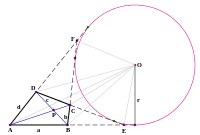
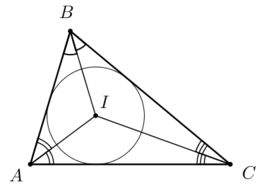
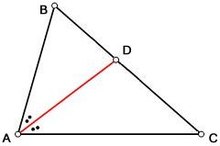
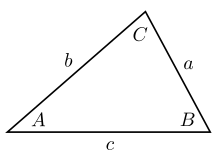
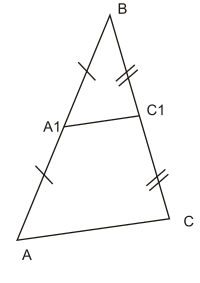
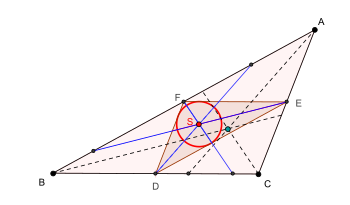
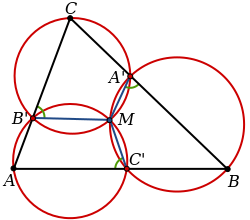
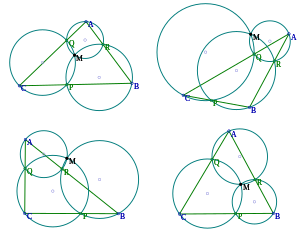
Пусть — треугольник с произвольными точками , и соответственно на сторонах , и (или на их продолжениях). Опишем три окружности около треугольников , , и Теорема Микеля утверждает, что эти три окружности пересекутся в одной точке , называемой точкой Микеля . Более того, будут равны друг другу три угла (отмечены на рисунке).
Частный случай
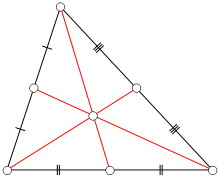
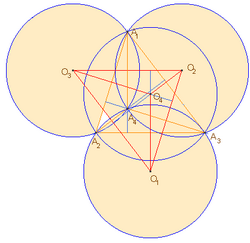
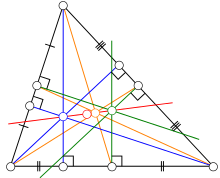
Если точка Микеля — центр описанной окружности треугольника, а диаметры трех окружностей Микеля равны радиусу описанной окружности треугольника, и каждая из трех окружностей Микеля проходит через общую для них точку — центр описанной окружности, а также через две проекции этого центра на стороны треугольника и через одну из трех вершин, тогда радиусы трех окружностей Микеля одинаковы.
См. также
- Точка Микеля — другой результат Микеля
Примечания
- , p. 94.
- Miquel, Auguste (1838), , , 1 : 485—487 13 февраля 2013 года.
- , p. 184 — Wells refers to Miquel’s theorem as the pivot theorem
Литература
- Coxeter, H.S.M.; Greitzer, S.L. (1967), Geometry Revisited , , vol. 19, Washington, D.C. : Mathematical Association of America , ISBN 978-0-88385-619-2 , Zbl
- Forder, H.G. (1960), Geometry , London: Hutchinson
- Ostermann, Alexander; Wanner, Gerhard (2012), Geometry by its History , Springer, ISBN 978-3-642-29162-3
- Pedoe, Dan (1988) [1970], Geometry / A Comprehensive Course , Dover, ISBN 0-486-65812-0
- Smart, James R. (1997), Modern Geometries (5th ed.), Brooks/Cole, ISBN 0-534-35188-3
- Wells, David (1991), The Penguin Dictionary of Curious and Interesting Geometry , New York: Penguin Books, ISBN 0-14-011813-6 , Zbl
- 2020-05-28
- 1