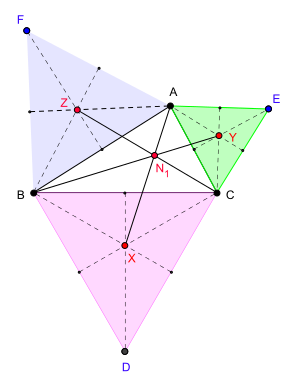
Точки Наполеона в геометрии — пара специальных точек на плоскости треугольника . Легенда приписывает обнаружение этих точек французскому императору Наполеону I , однако его авторство сомнительно . Точки Наполеона относятся к замечательным точкам треугольника и перечислены в Энциклопедии центров треугольника как точки X(17) и X(18).

Название «точки Наполеона» применяется также к различным парам центров треугольника, более известных как изодинамические точки .

Определение точек

Первая точка Наполеона

Пусть ABC — любой треугольник на плоскости . На сторонах BC , CA , AB треугольника строим внешние правильные треугольники DBC , ECA и FAB соответственно. Пусть центроиды этих треугольников — X , Y и Z соответственно. Тогда прямые AX , BY и CZ пересекаются в одной точке, и эта точка N1 является первой (или внешней) точкой Наполеона треугольника ABC .

Треугольник XYZ называется внешним треугольником Наполеона треугольника ABC . Теорема Наполеона утверждает, что этот треугольник является правильным .

В Энциклопедии центров треугольника первая точка Наполеона обозначена как X(17).

• Трилинейные координаты точки N1:

${\displaystyle {\begin{aligned}&\left(\csc \left(A+{\frac {\pi }{6}}\right),\csc \left(B+{\frac {\pi }{6}}\right),\csc \left(C+{\frac {\pi }{6}}\right)\right)\\&=\left(\sec \left(A-{\frac {\pi }{3}}\right),\sec \left(B-{\frac {\pi }{3}}\right),\sec \left(C-{\frac {\pi }{3}}\right)\right)\end{aligned}}}$

• Барицентрические координаты точки N1:

${\displaystyle \left(a\csc \left(A+{\frac {\pi }{6}}\right),b\csc \left(B+{\frac {\pi }{6}}\right),c\csc \left(C+{\frac {\pi }{6}}\right)\right)}$

Вторая точка Наполеона

Пусть ABC — любой треугольник на плоскости . На сторонах BC , CA , AB треугольника строим внутренние равносторонние треугольники DBC , ECA и FAB соответственно. Пусть X , Y и Z — центроиды этих треугольников соответственно. Тогда прямые AX , BY а CZ пересекаются в одной точке, и эта точка N2 является второй (или внутренней) точкой Наполеона треугольника ABC .

Треугольник XYZ называется внутренним треугольником Наполеона треугольника ABC . Теорема Наполеона утверждает, что этот треугольник является правильным .

В Энциклопедии центров треугольника вторая точка Наполеона обозначена как X(18).

• Трилинейные координаты точки N2:

${\displaystyle {\begin{aligned}&\left(\csc \left(A-{\frac {\pi }{6}}\right),\csc \left(B-{\frac {\pi }{6}}\right),\csc \left(C-{\frac {\pi }{6}}\right)\right)\\&=\left(\sec \left(A+{\frac {\pi }{3}}\right),\sec \left(B+{\frac {\pi }{3}}\right),\sec \left(C+{\frac {\pi }{3}}\right)\right)\end{aligned}}}$

• Барицентрические координаты точки N2:

${\displaystyle \left(a\csc \left(A-{\frac {\pi }{6}}\right),b\csc \left(B-{\frac {\pi }{6}}\right),c\csc \left(C-{\frac {\pi }{6}}\right)\right)}$

Две точки, тесно связанные с точками Наполеона — это точки Ферма (X13 и X14 в энциклопедии точек). Если вместо прямых, соединяющих центроиды равносторонних треугольников с соответствующими вершинами, провести прямые, соединяющие вершины равносторонних треугольников с соответствующими вершинами исходного треугольника, так построенные три прямые будут пересекаться в одной точке. Точки пересечения называются точками Ферма и обозначаются как F1 и F2. Пересечение прямой Ферма (то есть прямой, соединяющей две точки Ферма) и прямой Наполеона (то есть прямой, соединяющей две точки Наполеона) является симедианой треугольника (точка X6 в энциклопедии центров).

Свойства

• 

Гипербола Киперта — описанная гипербола, проходящая через центроид и ортоцентр . Если на сторонах треугольника построить подобные равнобедренные треугольники (наружу или внутрь), а затем соединить их вершины с противоположными вершинами исходного треугольника, то три такие прямые пересекутся в одной точке, лежащей на гиперболе Киперта. В частности, на этой гиперболе лежат точки Торричелли и точки Наполеона (точки пересечения чевиан, соединяющих вершины с центрами построенных на противоположных сторонах правильных треугольников) .

Обобщения

Результат о существовании точек Наполеона может быть обобщён различным образом. При определении точек Наполеона мы использовали равносторонние треугольники, построенные на сторонах треугольника ABC, а затем выбирали центры X, Y и Z этих треугольников. Эти центры можно рассматривать как вершины равнобедренных треугольников , построенных на сторонах треугольника ABC с углом при основании π/6 (30 градусов). Обобщения рассматривают другие треугольники, которые, будучи построенными на сторонах треугольника ABC, имеют аналогичные свойства, то есть прямые, соединяющие вершины построенных треугольников с соответствующими вершинами исходного треугольника, пересекаются в одной точке.

Равнобедренные треугольники

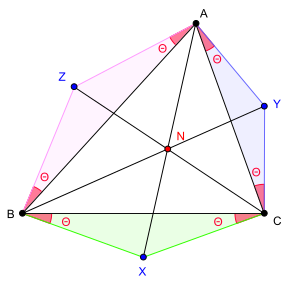
Это обобщение утверждает:

Если три треугольника XBC, YCA и ZAB построены на сторонах треугольника ABC, являются подобными , равнобедренными с основаниями на сторонах исходного треугольника, и одинаково расположенными (то есть все построены с внешней стороны, либо все построены с внутренней стороны), то прямые AX, BY и CZ пересекаются в одной точке N.

Если общий угол при основании равен ${\displaystyle \theta }$ , то вершины трёх треугольников имеют следующие трилинейные координаты.

• ${\displaystyle X(-\sin \theta ,\sin(C+\theta ),\sin(B+\theta ))}$
• ${\displaystyle Y(\sin(C+\theta ),-\sin \theta ,\sin(A+\theta ))}$
• ${\displaystyle Z(\sin(B+\theta ),\sin(A+\theta ),-\sin \theta )}$

Трилинейные координаты точки N

${\displaystyle (\csc(A+\theta ),\csc(B+\theta ),\csc(C+\theta ))}$

Несколько частных случаев.

Значение ${\displaystyle \theta }$	Точка ${\displaystyle N}$
0	G, центроид треугольника ABC (X2)
π /2 (или, — π /2)	O, ортоцентр треугольника ABC(X4)
${\displaystyle \mathrm {arctg} \,[\mathrm {tg} \,(A/2)\mathrm {tg} \,(B/2)\mathrm {tg} \,(C/2)]}$	Центр Шпикера (X10)
π /4	Внешняя точка Вектена(Vecten points) (X485)
— π /4	Внутренняя точка Вектена (Vecten points) (X486)
π /6	N1, первая точка Наполеона (X17)
- π /6	N2, вторая точка Наполеона (X18)
π /3	F1, первая точка Ферма (X13)
- π /3	F2, вторая точка Ферма (X14)
- A (если A < π /2) π — A (если A > π /2)	Вершина A
- B (если B < π /2) π — B (если B > π /2)	Вершина B
- C (если C < π /2) π — C (если C > π /2)	Вершина C

Более того, геометрическое место точек N при изменении угла при основании треугольников ${\displaystyle \theta }$ между -π/2 и π/2 является гиперболой

${\displaystyle {\frac {\sin(B-C)}{x}}+{\frac {\sin(C-A)}{y}}+{\frac {\sin(A-B)}{z}}=0,}$

где ${\displaystyle x,y,z}$ — трилинейные координаты точки N в треугольнике.

История

Эта гипербола называется гиперболой Киперта (в честь открывшего её немецкого математика Фридриха Вильгельма Августа Людвига Киперта (Friedrich Wilhelm August Ludwig Kiepert), 1846—1934 ). Эта гипербола является единственным коническим сечением, проходящим через точки A, B, C, G и O.

Замечание

Очень похожим свойством обладает Центр Шпикера . Центр Шпикера S является точкой пересечений прямых AX , BY и CZ , где треугольники XBC , YCA и ZAB подобные, равнобедренные и одинаково расположенные, построенные на сторонах треугольника ABC снаружи, имеющие один и тот же угол у основания ${\displaystyle \mathrm {arctg} \,[\mathrm {tg} \,(A/2)\mathrm {tg} \,(B/2)\mathrm {tg} \,(C/2)]}$ .

Подобные треугольники

Чтобы три прямые AX, BY и CZ пересекались в одной точке, треугольники XBC, YCA и ZAB, построенные на сторонах треугольника ABC, не обязательно должны быть равнобедренными .

Если подобные треугольники XBC, AYC и ABZ построены с внешних сторон на сторонах произвольного треугольника ABC, то прямые AX, BY и CZ пересекаются в одной точке.

Произвольные треугольники

Прямые AX, BY и CZ пересекаются в одной точке даже при более слабых условиях. Следующее условие является одним из наиболее общих условий, чтобы прямые AX, BY и CZ пересекались в одной точке .

Если треугольники XBC, YCA и ZAB построены с внешней стороны на сторонах треугольника ABC так, что

∠CBX = ∠ABZ, ∠ACY = ∠BCX, ∠BAZ = ∠CAY,

то прямые AX, BY и CZ пересекаются в одной точке.

Об открытии точек Наполеона

Коксетер и Грейтцер формулируют теорему Наполеона следующим образом: Если равносторонние треугольники построены с внешней стороны на сторонах любого треугольника, то их центры образуют равносторонний треугольник . Они замечают, что Наполеон Бонапарт был немного математиком и имел большой интерес к геометрии, однако они сомневаются, что он был достаточно геометрически образован, чтобы открыть теорему, приписываемую ему .

Самая ранняя сохранившаяся публикация с точками — статья в ежегодном журнале «The Ladies’ Diary» (Женский дневник, 1704—1841) в номере за 1825 год. Теорема входила в ответ на вопрос, посланный У. Резенфордом, однако в этой публикации Наполеон не упоминается.

В 1981 году немецкий историк математики Христоф Скриба ( Christoph J. Scriba ) опубликовал результаты исследования вопроса приписывания точек Наполеону в журнале .

См. также

• Теорема Ван-Обеля
• Точка Ферма
• Точки Вектена — пара треугольных центров, построенных аналогично точкам Наполеона с использованием квадратов вместо равносторонних треугольников.

Примечания

Литература

• J. F. Rigby . Napoleon revisited // Journal of Geometry. — 1988. — Т. 33 , вып. 1—2 . — С. 129—146 . — doi : .
• The Conics of Ludwig Kiepert: A Comprehensive Lesson in the Geometry of the Triangle // Mathematics Magazine. — 1994. — Т. 67 June , вып. 3 . — doi : .
• Michael de Villiers. Some Adventures in Euclidean Geometry. — Dynamic Mathematics Learning, 2009. — ISBN 9780557102952 .
• H. S. M. Coxeter, S. L. Greitzer. Geometry Revisited. — Mathematical Association of America, 1967. Перевод: Г. С. М. Коксетер, С. Л. Грейтцер. Новые встречи с геометрией. — Москва: «Наука», 1978. — (Библиотека математического кружка).
• Christoph J Scriba. Wie kommt 'Napoleons Satz' zu seinem namen? // Historia Mathematica. — 1981. — Т. 8 , вып. 4 . — doi : .
• Stachel, Hellmuth. (англ.) // Contributions to Algebra and Geometry : journal. — 2002. — Vol. 43 , no. 2 . — P. 433—444 .
• Grünbaum, Branko . (неопр.) // Geombinatorics . — 2001. — Т. 10 . — С. 116—121 .
• Katrien Vandermeulen, et al. (неопр.) Maths for Europe. Дата обращения: 25 апреля 2012. Архивировано из 30 августа 2012 года.
• Bogomolny, Alexander (неопр.) . Cut The Knot! An interactive column using Java applets. Дата обращения: 25 апреля 2012.
• (неопр.) . Дата обращения: 24 апреля 2012. Архивировано из 21 января 2012 года.
• Weisstein, Eric W. (неопр.) . From MathWorld—A Wolfram Web Resource. Дата обращения: 24 апреля 2012.
• Philip LaFleur (неопр.) . Дата обращения: 24 апреля 2012. 7 сентября 2012 года.
• Wetzel, John E. (неопр.) (апрель 1992). Дата обращения: 24 апреля 2012. 29 апреля 2014 года.