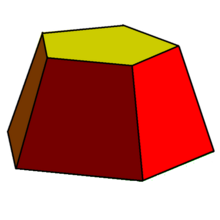
Усечённая пирами́да — многогранник , часть пирамиды , заключенная между основанием и плоскостью, параллельной основанию.

Связанные определения

• Основание изначальной пирамиды, а также параллельная ему грань называются основаниями усечённой пирамиды.
  • Остальные грани называются боковыми .

• Если изначальная пирамида правильная то её усечённая пирамида также называется правильной .
  • Высота боковой грани называется апофемой .

Свойства

• Боковые грани усечённой пирамиды представляют собой трапеции.

• Объём усечённой пирамиды равен ${\displaystyle V={\tfrac {1}{3}}\cdot h(S_{1}+{\sqrt {S_{1}\cdot S_{2}}}+S_{2})}$ , где ${\displaystyle S_{1},S_{2}}$ — площади оснований, ${\displaystyle h}$ — высота усечённой пирамиды.
  • Для квадратных усечённых пирамид эта формула была известна в Древнем Египте (задача № M14 Московского математического папируса ).

Правильная усечённая пирамида

• Боковые стороны правильной усечённой пирамиды, а также углы между ними и основанием усечённой пирамиды равны.
• Боковые грани правильной усечённой пирамиды являются равнобедренными трапециями, равными между собой.
• Равны двугранные углы между боковыми гранями, а также между каждой из граней и основанием усечённой пирамиды.
• Площадь боковой поверхности равна произведению полусуммы периметров её оснований и апофемы (высоты боковой грани): ${\displaystyle S_{b}={\frac {1}{2}}(p_{1}+p_{2})\cdot l}$ , где ${\displaystyle p_{1}}$ — периметр первого основания, ${\displaystyle p_{2}}$ — периметр второго, а ${\displaystyle l}$ — апофема.
• Площадь боковой поверхности равна ${\displaystyle S_{b}={\frac {|S_{1}-S_{2}|}{\cos \varphi }}}$ , где ${\displaystyle S_{1},S_{2}}$ — площади оснований, а ${\displaystyle \varphi }$ — двугранный угол при основании усечённой пирамиды.

В статье не хватает ссылок на источники (см. рекомендации по поиску ). Информация должна быть проверяема , иначе она может быть удалена. Вы можете статью, добавив ссылки на авторитетные источники в виде сносок . ( 26 ноября 2021 )