Геометрическое распределение

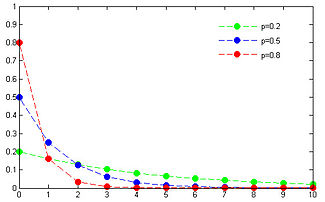
Функция вероятности
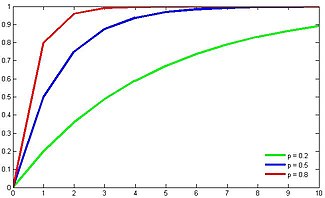
Функция распределения
Обозначение	${\displaystyle \mathrm {Geom} (p)}$
Параметры	${\displaystyle n\geq 0}$ — число «неудач» до первого «успеха» ${\displaystyle 0<p\leq 1}$ — вероятность «успеха» ${\displaystyle \ q\equiv 1-p}$ — вероятность «неудачи»	${\displaystyle n\geq 1}$ — номер первого «успеха» ${\displaystyle 0<p\leq 1}$ — вероятность «успеха» ${\displaystyle \ q\equiv 1-p}$ — вероятность «неудачи»
Носитель	${\displaystyle n\in \{0,1,2,3,\dots \}}$	${\displaystyle n\in \{1,2,3,\dots \}}$
Функция вероятности	${\displaystyle q^{n}p}$	${\displaystyle q^{n-1}p}$
Функция распределения	${\displaystyle 1-q^{n+1}}$	${\displaystyle 1-q^{n}}$
Математическое ожидание	${\displaystyle {\frac {q}{p}}}$	${\displaystyle {\frac {1}{p}}}$
Медиана	N/A	N/A
Мода	${\displaystyle 0}$	${\displaystyle 1}$
Дисперсия	${\displaystyle {\frac {q}{p^{2}}}}$	${\displaystyle {\frac {q}{p^{2}}}}$
Коэффициент асимметрии	${\displaystyle {\frac {2-p}{\sqrt {1-p}}}}$	${\displaystyle {\frac {2-p}{\sqrt {1-p}}}}$
Коэффициент эксцесса	${\displaystyle 6+{\frac {p^{2}}{1-p}}}$	${\displaystyle 6+{\frac {p^{2}}{1-p}}}$
Информационная энтропия	${\displaystyle -\log _{2}p-{\frac {q}{p}}\log _{2}{q}}$	${\displaystyle -\log _{2}p-{\frac {q}{p}}\log _{2}{q}}$
Производящая функция моментов	${\displaystyle {\frac {p}{1-qe^{t}}};t<-\ln(q)}$	${\displaystyle {\frac {pe^{t}}{1-qe^{t}}}}$
Характеристическая функция	${\displaystyle {\frac {p}{1-qe^{it}}}}$	${\displaystyle {\frac {pe^{it}}{1-qe^{it}}}}$

Под геометри́ческим распределе́нием в теории вероятностей подразумевают одно из двух распределений дискретной случайной величины :

• распределение вероятностей случайной величины ${\displaystyle X}$ равной номеру первого «успеха» в серии испытаний Бернулли и принимающей значения ${\displaystyle n=1,2,3,...}$ ;
• распределение вероятностей случайной величины ${\displaystyle Y=X-1}$ равной числу «неудач» до первого «успеха» и принимающей значения ${\displaystyle n=0,1,2,...}$ .

Определение

• Говорят, что случайная величина ${\displaystyle X}$ имеет геометрическое распределение с параметром ${\displaystyle p\in (0,1)}$ , и пишут ${\displaystyle \mathrm {Geom} _{1}(p)}$ , если принимает значения ${\displaystyle n=1,2,3,...}$ с вероятностями ${\displaystyle \mathbb {P} (X=n)=(1-p)^{n-1}p}$ . Случайная величина с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха ${\displaystyle p}$ .

• Пусть ${\displaystyle Z_{1},\ldots ,Z_{n},\ldots }$ — бесконечная последовательность независимых случайных величин с распределением Бернулли , то есть

${\displaystyle Z_{i}=\left\{{\begin{matrix}1,&p\\0,&q\equiv 1-p\end{matrix}}\right.,\;i=1,2,\ldots }$ .

Построим случайную величину ${\displaystyle Y=\min \left\{i\mid Z_{i}=1\right\}-1}$ — число «неудач» до первого «успеха». Распределение случайной величины ${\displaystyle Y}$ называется геометрическим с вероятностью «успеха» ${\displaystyle p}$ , что обозначается следующим образом: ${\displaystyle Y\sim \mathrm {Geom} _{0}(p)}$ . Функция вероятности случайной величины ${\displaystyle Y}$ имеет вид: ${\displaystyle \mathbb {P} (Y=n)=q^{n}p,\;n=0,1,2,\ldots }$ .

Замечание

• Иногда полагают по определению, что ${\displaystyle X}$ — номер первого «успеха». Тогда функция вероятности принимает форму ${\displaystyle \mathbb {P} (X=n)=q^{n-1}p,\;}$ где ${\displaystyle n=1,2,3,\ldots }$ . В таблице справа приведены формулы для обоих вариантов.
• Функция вероятности является геометрической прогрессией , откуда и происходит название распределения.

Моменты

Пусть ${\displaystyle X\sim \mathrm {Geom} _{1}(p)}$ и ${\displaystyle Y\sim \mathrm {Geom} _{0}(p)}$ . Тогда производящая функция моментов геометрического распределения имеет вид:

${\displaystyle M_{Y}(t)={\frac {pe^{t}}{1-qe^{t}}}}$ ,

откуда

${\displaystyle \mathbb {E} [X]={\frac {1}{p}}}$ ,

${\displaystyle \mathrm {D} [X]={\frac {q}{p^{2}}}}$ .

Справедливо, что ${\displaystyle \mathbb {E} [Y]=\mathbb {E} [X-1]={\frac {1}{p}}-1={\frac {1-p}{p}}={\frac {q}{p}}}$ .

Свойства геометрического распределения

• Из всех дискретных распределений с носителем ${\displaystyle \{1,2,3,\dots \}}$ и фиксированным средним ${\displaystyle \mu >1}$ геометрическое распределение ${\displaystyle \mathrm {Geom} (1/\mu )}$ является одним из распределений с максимальной информационной энтропией .
• Если ${\displaystyle X_{1},\ldots ,X_{n}}$ независимы и ${\displaystyle X_{i}\sim \mathrm {Geom} (p_{i}),\;i=1,\ldots ,n}$ , то

${\displaystyle X=\min \limits _{i}(X_{i})\sim \mathrm {Geom} \left(1-\prod \limits _{i=1}^{n}(1-p_{i})\right)}$ .

• Геометрическое распределение бесконечно делимо .

Отсутствие памяти

Если ${\displaystyle X\sim \mathrm {Geom} (p)}$ , то ${\displaystyle \mathbb {P} (X>m+n\mid X\geq m)=\mathbb {P} (X>n)\;,\forall m,n\in \mathbb {N} \cup \{0\}}$ , то есть число прошлых «неудач» не влияет на число будущих «неудач».

Геометрическое распределение — это единственное дискретное распределение со свойством .

Связь с другими распределениями

• Геометрическое распределение является частным случаем отрицательного биномиального распределения : ${\displaystyle \mathrm {Geom} (p)\equiv \mathrm {NB} (1,p)}$ .
• Если ${\displaystyle Y_{1},\ldots ,Y_{n}}$ независимы и ${\displaystyle Y_{i}\sim \mathrm {Geom} (p),\;i=1,\ldots ,n}$ , то

${\displaystyle \sum \limits _{i=1}^{n}Y_{i}\sim \mathrm {NB} (n,p)}$ .

• Если в отрицательном биномиальном распределении параметр r=1, то отрицательное биномиальное распределение становится геометрическим распределением. Последнее распределение является распределением Бозе-Эйнштейна для одного источника (a single source)

Пример

Пусть игральная кость кидается до выпадания первой шестёрки.

• Рассчитайте вероятность того, что число испытаний, проводимых до первого успеха, включая последнее, успешное испытание будет не больше трёх.

Положим ${\displaystyle X\sim \mathrm {Geom} _{1}(p=1/6)}$ . Тогда

${\displaystyle \mathbb {P} (X\leq 3)=\mathbb {P} (X=1)+\mathbb {P} (X=2)+\mathbb {P} (X=3)=}$

${\displaystyle =\left({\frac {5}{6}}\right)^{\!0}\left({\frac {1}{6}}\right)+\left({\frac {5}{6}}\right)^{\!1}\left({\frac {1}{6}}\right)+\left({\frac {5}{6}}\right)^{\!2}\left({\frac {1}{6}}\right)\approx 0{,}42}$ .

• Рассчитайте вероятность того, что число «неудач» до первого «успеха» будет не больше двух.

Положим ${\displaystyle Y\sim \mathrm {Geom} _{0}(p=1/6)}$ . Тогда

${\displaystyle \mathbb {P} (Y\leq 2)=\mathbb {P} (Y=0)+\mathbb {P} (Y=1)+\mathbb {P} (Y=2)=}$

${\displaystyle =\left({\frac {5}{6}}\right)^{0}\left({\frac {1}{6}}\right)+\left({\frac {5}{6}}\right)^{1}\left({\frac {1}{6}}\right)+\left({\frac {5}{6}}\right)^{2}\left({\frac {1}{6}}\right)\approx 0{,}42}$ .

См. также

• Биномиальное распределение .

Ссылки