Interested Article - Модель Форухи — Блумер

- 2021-06-05
- 1
Модель Форухи — Блумер — дисперсионные уравнения для среды с поглощением выведенные А. Р. Форухи и И. Блумер для комплексного показателя преломления n +i k , которые были опубликованы в 1986 и 1988 годах . Публикация 1986 г. относится к аморфным материалам, а публикация 1988 г. — к кристаллическим. Впоследствии, в 1991 году, их работа была включена в качестве главы в «Справочник оптических констант». Дисперсионные уравнения Форухи — Блумер описывают, как фотоны различной энергии взаимодействуют с тонкими плёнками. При использовании в спектроскопической дисперсионные уравнения Форухи — Блумер позволяют определять n (коэффициент преломления) и k (коэффициент поглощения) для аморфных и кристаллических материалов как функции энергии фотона E. Значения n(E) и k(E) называются спектрами n и k , которые также могут выражаться в зависимости от длины волны света λ, поскольку E = hc/λ , где h - постоянная Планка, а c — скорость света в вакууме. Вместе n и k часто называют «оптическими константами» материала (хотя они не являются константами, поскольку их значения зависят от энергии фотонов).
Уравнения
Вывод дисперсионных уравнений Форухи — Блумер основан на получении выражения для k как функции энергии фотона, символически записанного как k ( E ), исходя из первых принципов квантовой механики и физики твёрдого тела. Выражение для n как функции энергии фотона, символически записанное как n ( E ), затем определяется из выражения для k (E) в соответствии с соотношениями Крамерса — Кронига , которых гласят, что n (E) — это преобразование Гильберта k (E).
Аморфные материалы
Дисперсионные уравнения Форухи — Блумер для n ( E ) и k (E) для аморфных материалов имеют вид:
Каждый из пяти параметров A, B, C, E g и n (∞) имеет физическое значение . E g — ширина запрещённой зоны материала в оптическом диапазоне. A, B и C зависят от зонной структуры материала. Это положительные константы, такие что 4C-B 2 >0. Наконец, n(∞) — константа больше единицы, представляет собой значение n при E = ∞. Параметры B 0 и C 0 в уравнении для n (E) не являются независимыми параметрами, но зависят от основных параметров модели A, B, C и E g . Они задаются формулами:
где
Таким образом, для аморфных материалов нужно задать пять параметров, чтобы полностью описать зависимость как n, так и k от энергии фотона E .
Кристаллические материалы
Для кристаллических материалов, которые имеют несколько пиков в спектрах n и k , дисперсионные уравнения Форухи — Блумер обобщаются следующим образом:
Количество членов в каждой сумме q равно количеству пиков в n- и k- спектрах материала. Каждый член в сумме имеет свои собственные значения параметров A i , B i , C i , E g i , а также свои собственные значения B 0 i и C 0 i . Подобно аморфному случаю, все параметры имеют физическое значение .
Характеризация тонких плёнок
Показатель преломления ( n ) и коэффициент поглощения ( k ) связаны с взаимодействием между материалом и падающим светом и относятся к преломлению и поглощению света в материале, соответственно. Их можно рассматривать как «отпечатки пальцев» для материала. Покрытия из тонкоплёночного материала на различных подложках обеспечивают важные применения для , и n , k , а также толщина t этих тонкоплёночных составляющих должны измеряться и контролироваться для обеспечения воспроизводимости технологических процессов .
Изначально ожидалось, что дисперсионные уравнения Форухи — Блумер для n и k будут применяться к полупроводникам и диэлектрикам, будь то в аморфном, поликристаллическом или кристаллическом состояниях. Однако было показано, что они также описывают n- и k- спектры прозрачных проводников , а также металлических соединений . Было обнаружено, что этот формализм для кристаллических материалов применим также к полимерам , которые состоят из длинных цепочек молекул, не образующих кристаллографическую структуру в классическом смысле.
В литературе можно найти другие модели дисперсии, которые можно использовать для получения n и k , такие как Тауц — Лоренца . Две хорошо известные модели: Коши и Зелмейера предоставляют эмпирические выражения для n, действительные в ограниченном диапазоне частот, и полезны только для плёнок со слабым поглозщением, где k = 0. Следовательно, модель Форухи — Блумер используется для измерения тонких плёнок в различных приложениях .
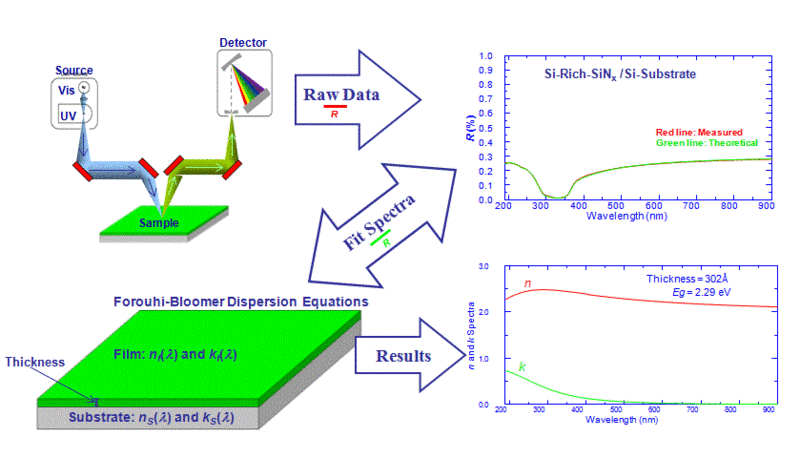
В следующих обсуждениях все переменные энергии фотонов E будут описаны в терминах длины волны света λ, поскольку экспериментальные переменные, связанные с тонкими плёнками, обычно измеряются по спектру длин волн. Спектры n и k тонкой плёнки нельзя измерить напрямую, их следует определять косвенно, исходя из измеряемых величин, которые зависят от них. Спектроскопическая отражательная способность, R(λ ), является одной из таких измеряемых величин. Другая величина — спектроскопический коэффициент пропускания T (λ) , применяется, когда подложка на которой расположена плёнка прозрачна. Спектроскопический коэффициент отражения тонкой плёнки на подложке представляет собой отношение интенсивности света, отражённого от образца, к интенсивности падающего света, измеренного в каком-то диапазоне длин волн, тогда как спектроскопический коэффициент пропускания, T (λ) , представляет собой отношение интенсивности света, прошедшего через образец, к интенсивности падающего света, измеренного в каком-то диапазоне длин волн; как правило, будет наблюдаться также отражённый сигнал R(λ) , сопровождающий T(λ) .
Измеримые величины R(λ) и T(λ) зависят не только от n(λ) и k(λ) плёнки, но также от толщины плёнки t , а также от n(λ) и k(λ) подложки . Для кремниевой подложки значения n(λ) и k(λ) известны и принимаются в качестве заданных входных данных. Задача определения характеристик тонких плёнок включает извлечение t , n(λ) и k(λ) плёнки из измерения R(λ) и/или T(λ) . Этого можно достичь, комбинируя дисперсионные уравнения Форухи — Блумер для n(λ) и k(λ) с уравнениями Френеля для отражения и пропускания света на границе раздела , чтобы получить теоретические, физически обоснованные выражения для коэффициента отражения и коэффициент пропускания. При этом задача сводится к получению пяти параметров A, B, C, E g и n(∞) , которые содержат n(λ) и k(λ), наряду с толщиной плёнки, t, за счёт использования нелинейного регрессионного анализ методом наименьших квадратов . Процедура подгонки влечёт за собой итеративное улучшение значений A, B, C, E g , n(∞) , t , чтобы уменьшить сумму квадратов ошибок между модельными R(λ) и T(λ) и измеренными спектрами R(λ) и T(λ) .
Помимо спектрального коэффициента отражения и пропускания, спектроскопическая эллипсометрия также может использоваться аналогичным образом для характеризации тонких плеёнок и определения t , n(λ) и k(λ) .
Примеры измерений
Следующие ниже примеры показывают универсальность использования дисперсионных уравнений Форухи — Блумер для характеристики тонких плёнок с использованием инструмента, основанного на спектроскопической отражательной способности, близкой к нормальному падению. Спектроскопическое пропускание, близкое к нормальному, также используется, когда подложка прозрачна. Спектры n(λ) и k(λ) каждой плёнки получают вместе с толщиной плёнки в широком диапазоне длин волн от глубокого ультрафиолетового до ближнего инфракрасного (190—1000 нм).
В следующих примерах обозначения теоретической и измеренной отражательной способностей на спектральных графиках выражаются как «R-theor» и «R-Meas», соответственно.
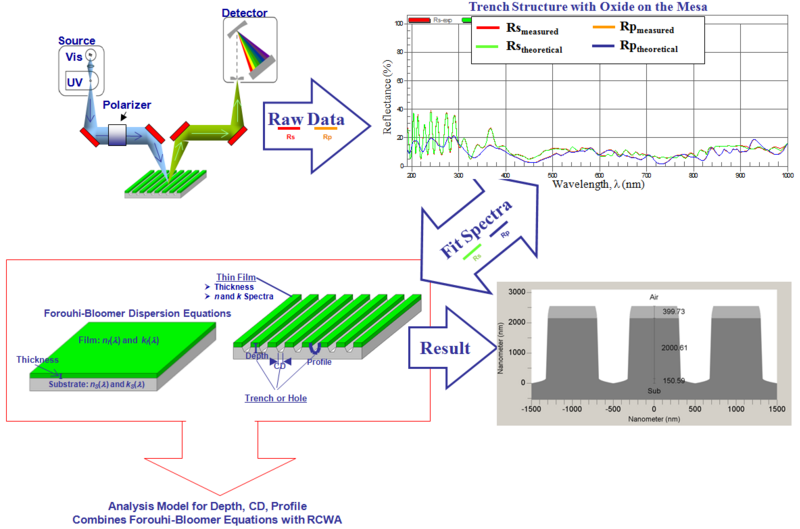
Ниже приведены схемы, изображающие процесс измерения тонких плёнок:
Уравнения дисперсии Форухи — Блумер в сочетании со также использовались для получения подробной информации о профиле (глубина, CD, угол боковой стенки) траншейных поверхностных структур. Для извлечения структурной информации данные поляризованного широкополосного отражения, Rs и Rp , должны быть измерены в большом диапазоне длин волн из периодической структуры (решётки), а затем проанализированы с помощью модели, которая включает дисперсионные уравнения Форухи — Блумер и RCWA. Входные данные для модель включают шаг решётки и n- и k- спектры всех материалов в структуре, в то время как выходные данные могут включать глубину, CD в нескольких местах и даже угол боковой стенки. Спектры n и k таких материалов могут быть получены в соответствии с методологией, описанной в этом разделе для измерений тонких плёнок.
Ниже приведены схемы, изображающие процесс измерения траншейных поверхностных структур. Далее следуют примеры измерения траншеи.
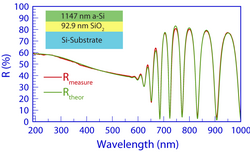
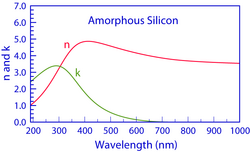
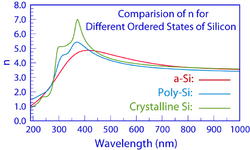
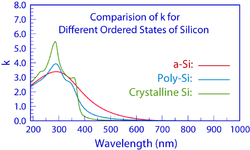
В рисунке 1 показан один широкий максимум в спектрах n(λ) и k(λ) плёнки a-Si, как и ожидалось для аморфных материалов. По мере перехода материала к кристалличности широкий максимум сменяется несколькими более резкими пиками в его спектрах n(λ) и k(λ) , как показано на графиках.
Когда измерение включает две или более плёнки в стопке плёнок, теоретическое выражение для коэффициента отражения должно быть расширено, чтобы включить спектры n(λ) и k(λ) плюс толщину t каждой плёнки. Однако регрессия может не сходиться к уникальным значениям параметров из-за нелинейного характера выражения для отражательной способности. Так что полезно исключить некоторые из неизвестных. Например, спектры n(λ) и k(λ) одной или нескольких плёнок могут быть известны из литературы или предыдущих измерений и удерживаться фиксированными (не могут изменяться) во время регрессии. Для получения результатов, показанных на рисунке 1, спектры n(λ) и k(λ) слоя SiO 2 были фиксированы, а другие параметры, n(λ) и k(λ) a-Si, плюс толщина как a-Si, так и SiO 2 можно было изменять.
Примечания
- ↑ Forouhi, A.R. (1986). "Optical Dispersion Relations for Amorphous Semiconductors and Amorphous Dielectrics". Physical Review B . 34 (10): 7018—7026. Bibcode : . doi : . PMID .
- ↑ Forouhi, A.R. (1988). "Optical Properties of Crystalline Semiconductors and Dielectrics". Physical Review B . 38 (3): 1865—1874. Bibcode : . doi : .
- Roman, P. . — Addison-Wesley, 1965.
- ↑ Torkaman, N.M. (2010). "Crystallographic Parameters and Electro-Optical Constants in ITO Thin Films". Materials Characterization . 61 (3): 362—370. doi : .
- ↑ Lakhdar, M.H. (2014). "Thickness Effect on the Structural and Optical Constants of Stibnite Thin Films Prepared by Sulfidation Annealing of Antimony Films". Optik – International Journal for Light and Electron Optics .
- ↑ Al-Khanbashi, H.A. (2014). "Spectroscopic Ellipsometry of Zn1−xCuxO Thin Films Based on a Modified Sol–Gel Dip-Coating Technique". Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy . 118 : 800—805. Bibcode : . doi : . PMID .
- ↑ Nakamura, T. (2014). "Emission Decay Rate of a Light Emitter on Thin Metal Films". Japanese Journal of Applied Physics . 53 (4). Bibcode : . doi : .
- ↑ Winkler, M.T. (2014). "Optical Designs that Improve the Efficiency of Cu2ZnSn(S,Se)4 Solar Cells". Energy & Environmental Science . 7 (3): 1029—1036. doi : .
- ↑ Miao, L. (2013). "Cost-Effective Nanoporous SiO2–TiO2 Coatings on Glass Substrates with Antireflective and Self-Cleaning Properties". Applied Energy . 112 : 1198—1205. doi : .
- ↑ Zhang, F. (2013). "Temperature-Dependent Optical Properties of Titanium Oxide Thin Films Studied by Spectroscopic Ellipsometry". Applied Physics Express . 6 (12). Bibcode : . doi : .
- ↑ Sheng-Hong, Y. (2013). "Optical Study of Sol-gel Processed Nd-doped BiFeO3 Multiferroic Films by Spectroscopic Ellipsometry". Ferroelectrics . 454 (1): 78—83. doi : .
- ↑ Balakrishnan, G. (2011). "A Study of Microstructural and Optical Properties of Nanocrystalline Ceria Thin Films Prepared by Pulsed Laser Deposition". Thin Solid Films . 519 (8): 2520—2526. Bibcode : . doi : .
- ↑ Cheng, K.W. (2010). "Effect of Sb on the growth and photoelectrochemical response of AgIn5S8 Film Electrodes Created by Solution Growth Technique". Chemical Engineering Science . 65 (1): 74—79. doi : .
- ↑ Das, N.S. (2010). "Effect of Film Thickness on the Energy Band Gap of Nanocrystalline CdS Thin Films Analyzed by Spectroscopic Ellipsometry". Physica E: Low-dimensional Systems and Nanostructures . 42 (8): 2097—2102. Bibcode : . doi : .
- ↑ Xiong, K. (2014). "Phosphor-Doping Enhanced Efficiency in Bilayer Organic Solar Cells due to Longer Exciton Diffusion Length". Journal of Luminescence . 151 : 193—196. Bibcode : . doi : .
- ↑ Huynh, T.P. (2013). "Electrochemically Synthesized Molecularly Imprinted Polymer of Thiophene Derivatives for Flow-Injection Analysis Determination of Adenosine-5′-Triphosphate (ATP)". Biosensors and Bioelectronics . 41 : 634—641. doi : . PMID .
- ↑ Zhu, D. (2008). "Determination of the Optical Constants of Polymer Light-Emitting Diode Films from Single Reflection Measurements". Journal of Physics D: Applied Physics . 41 (23). Bibcode : . doi : .
- Laidani, N. (2008). "Optical Absorption Parameters of Amorphous Carbon Films from Forouhi–Bloomer and Tauc–Lorentz Models: A Comparative Study". Journal of Physics: Condensed Matter . 20 (1). Bibcode : . doi : .
- Easwarakhanthan, T. (2007). "Forouhi–Bloomer and Tauc–Lorentz Optical Dispersions Applied Using Spectroscopic Ellipsometry to Plasma-Deposited Fluorocarbon Films". Journal of Applied Physics . 101 (7): 073102–073102–7. Bibcode : . doi : .
- Heavens, O.S. . — New York : Dover, 1965.
- Levenberg, K. (1944). "A Method for the Solution of Certain Non-Linear Problems in Least Squares". The Quarterly of Applied Mathematics . 2 (2). doi : .
- Marquardt, D.W. (1963). "An Algorithm for Least-Squares Estimation of Nonlinear Parameters". Journal of the Society for Industrial and Applied Mathematics . 11 (2): 431—441. doi : .
- 2021-06-05
- 1



![{\displaystyle C_{0}={\frac {A}{Q}}\ \left[({E_{g}}^{2}+C){\frac {B}{2}}\ -2E_{g}C\right]\,,}](/images/005/546/5546367/4.jpg?rand=274617)

![{\displaystyle k(E)=\sum _{i=1}^{q}\left[{\frac {A_{i}(E-E_{g_{i}})^{2}}{E^{2}-B_{i}E+C_{i}}}\right]\,,}](/images/005/546/5546367/6.jpg?rand=844758)
![{\displaystyle n(E)=n(\infty )+\sum _{i=1}^{q}\left[{\frac {B_{0_{i}}E+C_{0_{i}}}{E^{2}-B_{i}E+C_{i}}}\right]\,.}](/images/005/546/5546367/7.jpg?rand=362597)