Пространство состояний — в теории управления один из основных методов описания поведения динамической системы. Движение системы в пространстве состояний отражает изменение её состояний .

Определение

Пространство состояний обычно называют фазовым пространством динамической системы , а траекторию движения изображающей точки в этом пространстве — фазовой траекторией .

В пространстве состояний создаётся модель динамической системы , включающая набор переменных входа, выхода и состояния , связанных между собой дифференциальными уравнениями первого порядка, которые записываются в матричной форме. В отличие от описания в виде передаточной функции и других методов частотной области, пространство состояний позволяет работать не только с линейными системами и нулевыми начальными условиями. Кроме того, в пространстве состояний относительно просто работать с MIMO -системами.

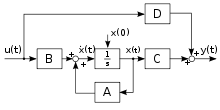
Линейные непрерывные системы

Для случая линейной системы с ${\displaystyle p}$ входами, ${\displaystyle q}$ выходами и ${\displaystyle n}$ переменными состояния описание имеет вид:

${\displaystyle {\dot {\mathbf {x} }}(t)=A(t)\mathbf {x} (t)+B(t)\mathbf {u} (t)}$

${\displaystyle \mathbf {y} (t)=C(t)\mathbf {x} (t)+D(t)\mathbf {u} (t)}$

где

${\displaystyle x(t)\in \mathbb {R} ^{n}}$ ; ${\displaystyle y(t)\in \mathbb {R} ^{q}}$ ; ${\displaystyle u(t)\in \mathbb {R} ^{p}}$ ;

${\displaystyle \operatorname {dim} [A(\cdot )]=n\times n}$ , ${\displaystyle \operatorname {dim} [B(\cdot )]=n\times p}$ , ${\displaystyle \operatorname {dim} [C(\cdot )]=q\times n}$ , ${\displaystyle \operatorname {dim} [D(\cdot )]=q\times p}$ , ${\displaystyle {\dot {\mathbf {x} }}(t):={d\mathbf {x} (t) \over dt}}$ :

${\displaystyle x(\cdot )}$ — вектор состояния , элементы которого называются состояниями системы

${\displaystyle y(\cdot )}$ — вектор выхода ,

${\displaystyle u(\cdot )}$ — вектор управления ,

${\displaystyle A(\cdot )}$ — матрица системы ,

${\displaystyle B(\cdot )}$ — матрица управления ,

${\displaystyle C(\cdot )}$ — матрица выхода,

${\displaystyle D(\cdot )}$ — матрица прямой связи .

Часто матрица ${\displaystyle D(\cdot )}$ является нулевой, это означает, что в системе нет явной .

Дискретные системы

Для дискретных систем запись уравнений в пространстве основывается не на дифференциальных , а на уравнениях:

${\displaystyle \mathbf {x} (nT+T)=A(nT)\mathbf {x} (nT)+B(nT)\mathbf {u} (nT)}$

${\displaystyle \mathbf {y} (nT)=C(nT)\mathbf {x} (nT)+D(nT)\mathbf {u} (nT)}$

Нелинейные системы

Нелинейная динамическая система n-го порядка может быть описана в виде системы из n уравнений 1-го порядка:

${\displaystyle {\dot {x}}_{1}=f_{1}(x_{1}(t);\ldots ,x_{n}(t),u_{1}(t),\ldots ,u_{m}(t))}$

${\displaystyle \vdots }$

${\displaystyle {\dot {x}}_{n}=f_{n}(x_{1}(t);\ldots ,x_{n}(t),u_{1}(t),\ldots ,u_{m}(t))}$

или в более компактной форме:

${\displaystyle \mathbf {\dot {x}} (t)=\mathbf {f} (t,\mathbf {x} (t),\mathbf {u} (t))}$

${\displaystyle \mathbf {y} (t)=\mathbf {h} (t,\mathbf {x} (t),\mathbf {u} (t))}$ .

Первое уравнение — это уравнение состояния , второе — уравнение выхода .

Линеаризация

В некоторых случаях возможна линеаризация описания динамической системы для окрестности рабочей точки ${\displaystyle (\mathbf {\tilde {x}} ,\mathbf {\tilde {u}} )}$ . В установившемся режиме ${\displaystyle (\mathbf {\tilde {u}} =const)}$ для рабочей точки ${\displaystyle \mathbf {\tilde {x}} =const,}$ справедливо следующее выражение:

${\displaystyle \mathbf {\dot {x}} =\mathbf {f} (\mathbf {\tilde {x}} ,\mathbf {\tilde {u}} )=\mathbf {0} }$

Вводя обозначения:

${\displaystyle \delta \mathbf {u} =\mathbf {u} -\mathbf {\tilde {u}} }$

${\displaystyle \delta \mathbf {x} =\mathbf {x} -\mathbf {\tilde {x}} }$

Разложение уравнения состояния ${\displaystyle \mathbf {f} (\mathbf {x} (t),\mathbf {u} (t))}$ в ряд Тейлора , ограниченное первыми двумя членами даёт следующее выражение:

${\displaystyle \mathbf {f} (\mathbf {x} (t),\mathbf {u} (t))\approx \mathbf {f} (\mathbf {\tilde {x}} (t),\mathbf {\tilde {u}} (t))+{\frac {\delta \mathbf {f} }{\delta \mathbf {x} }}\delta \mathbf {x} +{\frac {\delta \mathbf {f} }{\delta \mathbf {u} }}\delta \mathbf {u} }$

При взятии частных производных вектор-функции ${\displaystyle \mathbf {f} }$ по вектору переменных состояний ${\displaystyle \mathbf {x} }$ и вектору входных воздействий ${\displaystyle \mathbf {u} }$ получаются матрицы Якоби соответствующих систем функций:

${\displaystyle {\frac {\delta \mathbf {f} }{\delta \mathbf {x} }}={\begin{bmatrix}{\frac {\delta \mathbf {f_{1}} }{\delta \mathbf {x_{1}} }}&\cdots &{\frac {\delta \mathbf {f_{1}} }{\delta \mathbf {x_{n}} }}\\\vdots &\ddots &\vdots \\{\frac {\delta \mathbf {f_{n}} }{\delta \mathbf {x_{1}} }}&\cdots &{\frac {\delta \mathbf {f_{n}} }{\delta \mathbf {x_{n}} }}\end{bmatrix}}\quad {\frac {\delta \mathbf {f} }{\delta \mathbf {u} }}={\begin{bmatrix}{\frac {\delta \mathbf {f_{1}} }{\delta \mathbf {u_{1}} }}&\cdots &{\frac {\delta \mathbf {f_{1}} }{\delta \mathbf {u_{p}} }}\\\vdots &\ddots &\vdots \\{\frac {\delta \mathbf {f_{n}} }{\delta \mathbf {u_{1}} }}&\cdots &{\frac {\delta \mathbf {f_{n}} }{\delta \mathbf {u_{p}} }}\end{bmatrix}}}$ .

Аналогично для функции выхода:

${\displaystyle {\frac {\delta \mathbf {h} }{\delta \mathbf {x} }}={\begin{bmatrix}{\frac {\delta \mathbf {h_{1}} }{\delta \mathbf {x_{1}} }}&\cdots &{\frac {\delta \mathbf {h_{1}} }{\delta \mathbf {x_{n}} }}\\\vdots &\ddots &\vdots \\{\frac {\delta \mathbf {h_{q}} }{\delta \mathbf {x_{1}} }}&\cdots &{\frac {\delta \mathbf {h_{q}} }{\delta \mathbf {x_{n}} }}\end{bmatrix}}\quad {\frac {\delta \mathbf {h} }{\delta \mathbf {u} }}={\begin{bmatrix}{\frac {\delta \mathbf {h_{1}} }{\delta \mathbf {u_{1}} }}&\cdots &{\frac {\delta \mathbf {h_{1}} }{\delta \mathbf {u_{p}} }}\\\vdots &\ddots &\vdots \\{\frac {\delta \mathbf {h_{q}} }{\delta \mathbf {u_{1}} }}&\cdots &{\frac {\delta \mathbf {h_{q}} }{\delta \mathbf {u_{p}} }}\end{bmatrix}}}$

Учитывая ${\displaystyle \delta \mathbf {\dot {x}} =\mathbf {\dot {x}} -\mathbf {\dot {\tilde {x}}} =\mathbf {\dot {x}} }$ , линеаризованное описание динамической системы в окрестности рабочей точки примет вид:

${\displaystyle \mathbf {\dot {x}} }$	${\displaystyle =\mathbf {A} \delta \mathbf {x} +\mathbf {B} \delta \mathbf {u} }$
${\displaystyle \delta \mathbf {y} }$	${\displaystyle =\mathbf {C} \delta \mathbf {x} +\mathbf {D} \delta \mathbf {u} }$

где

${\displaystyle \mathbf {A} ={\frac {\delta \mathbf {f} }{\delta \mathbf {x} }}\quad \mathbf {B} ={\frac {\delta \mathbf {f} }{\delta \mathbf {u} }}\quad \mathbf {C} ={\frac {\delta \mathbf {h} }{\delta \mathbf {x} }}\quad \mathbf {D} ={\frac {\delta \mathbf {h} }{\delta \mathbf {u} }}}$ .

Примеры

Модель в пространстве состояний для маятника

Маятник является классической свободной нелинейной системой . Математически движение маятника описывается следующим соотношением:

${\displaystyle ml{\ddot {\theta }}(t)=-mg\sin \theta (t)-kl{\dot {\theta }}(t)}$

где

• ${\displaystyle \theta (t)}$ — угол отклонения маятника.
• ${\displaystyle m}$ — приведённая масса маятника
• ${\displaystyle g}$ — ускорение свободного падения
• ${\displaystyle k}$ — коэффициент трения в подшипнике подвеса
• ${\displaystyle l}$ — длина подвеса маятника

В таком случае уравнения в пространстве состояний будут иметь вид:

${\displaystyle {\dot {x_{1}}}(t)=x_{2}(t)}$

${\displaystyle {\dot {x_{2}}}(t)=-{\frac {g}{l}}\sin {x_{1}}(t)-{\frac {k}{m}}{x_{2}}(t)}$

где

• ${\displaystyle x_{1}(t):=\theta (t)}$ — угол отклонения маятника
• ${\displaystyle x_{2}(t):={\dot {x_{1}}}(t)}$ — угловая скорость маятника
• ${\displaystyle {\dot {x_{2}}}(t):={\ddot {x_{1}}}(t)}$ — угловое ускорение маятника

Запись уравнений состояния в общем виде:

${\displaystyle {\dot {\mathbf {x} }}(t)=\left({\begin{matrix}{\dot {x_{1}}}(t)\\{\dot {x_{2}}}(t)\end{matrix}}\right)=\mathbf {f} (t,x(t))=\left({\begin{matrix}x_{2}(t)\\-{\frac {g}{l}}\sin {x_{1}}(t)-{\frac {k}{m}}{x_{2}}(t)\end{matrix}}\right)}$ .

Линеаризация модели маятника

Линеаризованная матрица системы для модели маятника в окрестности точки равновесия ${\displaystyle \left({\tilde {x}}_{1}=0\right)}$ имеет вид:

${\displaystyle {\frac {\delta \mathbf {f} }{\delta \mathbf {x} }}=\left({\begin{matrix}0&\ 1\\-{\frac {g}{l}}\cos {{\tilde {x}}_{1}}&\ -{\frac {k}{m}}\end{matrix}}\right)=\left({\begin{matrix}0&\ 1\\-{\frac {g}{l}}&\ -{\frac {k}{m}}\end{matrix}}\right)}$

При отсутствии трения в подвесе ( k = 0 ) получим уравнение движения математического маятника :

${\displaystyle {\ddot {x}}=-{\frac {g}{l}}x}$

См. также

Литература

• Книги

• Статьи

Ссылки