Interested Article - Синхронизирующее слово
- 2021-07-06
- 2
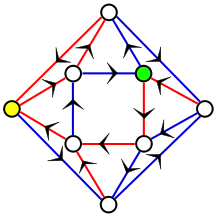
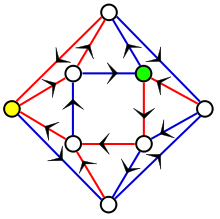
В информатике , точнее, в теории детерминированных конечных автоматов (ДКА), синхронизирующее слово (или сжимающая последовательность ) во входном алфавите автомата отображает все его состояния в одно и то же состояние . То есть, если слово стартует на ансамбле всех состояний автомата, проходя все ориентированные дуги с одинаковой скоростью, все пути завершатся одновременно в одном и том же состоянии. Не у каждого ДКА есть синхронизирующее слово, например, ДКА с двумя состояниями и циклами длины два никогда не могут быть синхронизированы.
Проблема оценки длины синхронизирующего слова имеет долгую историю и была поставлена независимо несколькими авторами, но широко известной стала как гипотеза Черны. В 1964 году Ян Черны предположил, что (N — 1) 2 является точной верхней границей для длины кратчайшего синхронизирующего слова для любого ДКА с N состояниями и К разноцветными исходящими ребрами из каждой вершины (ДКА с полным графом переходов). Черны еще в 1964 году нашел класс автоматов (с числом N состояний для любого натурального N), у которых кратчайшее синхронизирующее слово имеет эту длину. Лучшая известная верхняя граница для этой длины на сегодня равна (N 3 — N) / 6 и далека от нижней границы.
Для ДКА с N состояниями над алфавитом из K символов, алгоритм Дэвида Эпстайна находит синхронизирующее слово за время O(N 3 + n 2 k) и с объемом памяти O(n 2 ) . В этой статье также доказана NP—полнота нахождения синхронизирующего слова минимальной длины.
Проблема раскраски дорог является проблемой раскраски ребер регулярного ориентированного графа символами (цветами) входного алфавита из K символов, (где К является также полустепенью исхода каждой вершины) с целью формирования синхронизируемого ДКА. Бенджамин Вайсс и Рой Адлер в 1970 году высказали гипотезу, что у любого сильно связного орграфа с постоянной полустепенью исхода каждой вершины и равным единице наибольшим общим делителем длин всех циклов существует синхронизирующая раскраска . Их гипотеза была доказана в 2007 году Абрамом Трахтманом .
Примечания
- ↑ Černý, J. (1964), «Poznámka k homogénnym eksperimentom s konecnými automatami», Matematicko-fyzikálny Časopis Slovenskej Akadémie Vied 14: 208—216. (словацк.)
- Eppstein, David (1990), «Reset Sequences for Monotonic Automata», SIAM Journal on Computing 19: 500—510
- Adler, R. L.; Weiss, B. (1970), «Similarity of automorphisms of the torus», Memoires of the American Mathematical Society 98.
- Trahtman, Avraham (2007), The road coloring problem, Israel J. of Math. , 172(1), 2009, 51-60.
- 2021-07-06
- 2