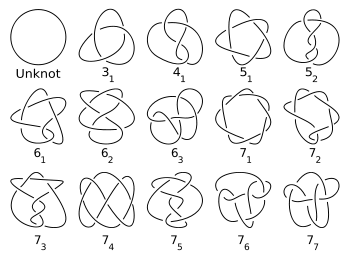
Простóй у́зел (простóе зацеплéние) в теории узлов — узел , который, в определённом смысле, — неразложим. Точнее, это нетривиальный узел, который нельзя представить в виде конкатенации двух нетривиальных узлов. Об узлах, не являющихся простыми, говорят как о составных узлах или составных зацеплениях . Определить, является ли данный узел простым или нет, может оказаться сложной задачей.

Примеры

Хорошим примером семейства простых узлов служат торические узлы . Эти узлы образуются накручиванием окружности на тор p раз в одном направлении и q раз в другом, где p и q являются взаимно простыми целыми числами .

Простейший простой узел — это трилистник с тремя пересечениями. Трилистник является, фактически, (2, 3)-торическим узлом. Узел «восьмёрка» с четырьмя пересечениями является простейшим неторическим узлом. Для любого положительного целого числа n имеется конечное число простых узлов с n пересечениями . Первые несколько значений числа простых узлов (последовательность в OEIS ) даны в следующей таблице.

Заметим, что антиподы считались в этой таблице и ниже лежащем рисунке только один раз (т. е. узел и его зеркальное отражение считаются эквивалентными).

Теорема Шуберта

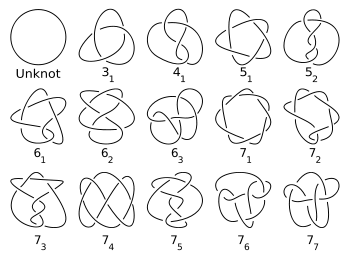
Теорема, принадлежащая Хорсту Шуберту, утверждает, что любой узел можно единственным образом представить в виде конкатенации простых узлов .

См. также

Примечания

Литература

• H. Schubert. Die eindeutige Zerlegbarkeit eines Knotens in Primknoten // S.-B Heidelberger Akad. Wiss. Math.-Nat. Kl. — 1949.

Ссылки

• Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
• [Prime Links with a Non-Prime Component ]Knot Atlas