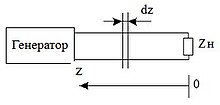
Длинная линия — модель линии передачи , продольный размер (длина) которой превышает длину волны , распространяющейся в ней (либо сравнима с длиной волны), а поперечные размеры (например, расстояние между проводниками, образующими линию) значительно меньше длины волны.

С точки зрения теории электрических цепей длинная линия относится к четырёхполюсникам . Характерной особенностью длинной линии является проявление интерференции двух волн, распространяющихся навстречу друг другу. Одна из этих волн создается подключенным ко входу линии генератором электромагнитных колебаний и называется падающей . Другая волна называется отражённой и возникает из-за частичного отражения падающей волны от нагрузки, подключенной к выходу (противоположному генератору концу) линии. Всё разнообразие колебательных и волновых процессов, происходящих в длинной линии, определяется соотношениями амплитуд и фаз падающей и отраженной волн. Анализ процессов упрощается, если длинная линия является регулярной , то есть такой, у которой в продольном направлении неизменны поперечное сечение и электромагнитные свойства (ε _r , μ _r , σ) заполняющих сред .

Дифференциальные уравнения длинной линии

Первичные параметры

Из электродинамики известно, что линия передачи может быть охарактеризована её погонными параметрами :

• R ₁ — погонное сопротивление металла проводов, Ом/м ;
• G ₁ — паразитная, параллельная( ) погонная(продольная, аддитивная) проводимость диэлектрика линии, 1/Ом·м или См /м; ,- погонная вдоль линии, ортогонально токам утечки через диэлектрик, в противовес g[Cм·м] - проводимости погонной,приведённой к единице длины паразитного тока, текущего через диэлектрик линии(поперечно-погонной проводимости изолятора линии)!
• L ₁ — погонная индуктивность Гн/м ;
• C ₁ — погонная ёмкость Ф/м ;
• ${\displaystyle Z_{1}=R_{1}+i\omega L_{1}}$
• ${\displaystyle Y_{1}=G_{1}+i\omega C_{1}}$

Погонные сопротивление и проводимость G ₁ зависят от проводимости материала проводов и качества диэлектрика, окружающего эти провода, соответственно. Согласно закону Джоуля — Ленца , чем меньше тепловые потери в металле проводов и в диэлектрике, тем меньше погонное сопротивление металла R ₁ и меньше погонная проводимость диэлектрика G ₁ . (Уменьшение активных потерь в диэлектрике означает увеличение его сопротивления, так как активные потери в диэлектрике — это токи утечки. Для модели используется обратная величина — погонная проводимость G ₁ .)

Погонные индуктивность L ₁ и ёмкость C ₁ определяются формой и размерами поперечного сечения проводов, а также расстоянием между ними.

А ${\displaystyle Z_{1}}$ и ${\displaystyle Y_{1}}$ — погонные комплексные сопротивление и проводимость линии, зависящие от частоты ${\displaystyle \omega }$ .

Выделим из линии элементарный участок бесконечно малой длины dz и рассмотрим его эквивалентную схему.

Эквивалентная схема участка длинной линии

Значения параметров схемы определяются соотношениями:

${\displaystyle {\begin{cases}dR=R_{1}dz;\\dG=G_{1}dz;\\dL=L_{1}dz;\\dC=C_{1}dz;\\\end{cases}}}$

(1)

Используя эквивалентную схему, запишем выражения для приращений напряжения и тока:

${\displaystyle {\begin{cases}dU=-I(dR+i\omega dL)\\dI=-U(dG+i\omega dC)\\\end{cases}}}$

Подставляя сюда значения параметров схемы из (1), получаем:

${\displaystyle {\begin{cases}dU=-IZ_{1}dz\\dI=-UY_{1}dz\\\end{cases}}}$

Из последних соотношений находим дифференциальные уравнения линии. Эти уравнения определяют связь между током и напряжением в любом сечении линии и называются телеграфными уравнениями длинной линии:

Телеграфные уравнения

${\displaystyle {\begin{cases}{\frac {dU}{dz}}=-IZ_{1}\\{\frac {dI}{dz}}=-UY_{1}\\\end{cases}}}$

(2)

Следствия

Решим телеграфные уравнения относительно напряжения и тока. Для этого продифференцируем их по z :

${\displaystyle {\begin{cases}{\frac {d^{2}U}{dz^{2}}}=-{\frac {dI}{dz}}Z_{1}\\{\frac {d^{2}I}{dz^{2}}}=-{\frac {dU}{dz}}Y_{1}\\\end{cases}}}$

(3)

При этом учтем условие регулярности линии:

Условие регулярности линии

${\displaystyle {\begin{cases}{\frac {dZ_{1}}{dz}}=0\\{\frac {dY_{1}}{dz}}=0\\\end{cases}}}$

(4)

Данные соотношения являются математическим определением регулярности длинной линии. Смысл соотношения (4) состоит в неизменности вдоль линии её погонных параметров.

Подставляя в (3) значения производных напряжения и тока из (2), после преобразований получаем:

Однородные волновые уравнения длинной линии

${\displaystyle {\begin{cases}{\frac {d^{2}U}{dz^{2}}}-\gamma ^{2}U=0\\{\frac {d^{2}I}{dz^{2}}}-\gamma ^{2}I=0\\\end{cases}}}$ ,

(5)

где ${\displaystyle \gamma ={\sqrt {Z_{1}Y_{1}}}}$ — коэффициент распространения волны в линии.

Соотношения (5) называются однородными волновыми уравнениями длинной линии . Их решения известны и могут быть записаны в виде:

${\displaystyle {\begin{cases}U=B_{U}e^{\gamma z}+A_{U}e^{-\gamma z}\\I=B_{I}e^{\gamma z}+A_{I}e^{-\gamma z}\\\end{cases}}}$ ,

(6)

где A _U , B _U и A _I , B _I — коэффициенты, имеющие единицы измерения напряжения и тока соответственно, смысл которых будет ясен ниже.

Решения волновых уравнений в виде (6) имеют весьма характерный вид: первое слагаемое в этих решениях представляет собой отраженную волну напряжения или тока, распространяющуюся от нагрузки к генератору, второе слагаемое — падающую волну, распространяющуюся от генератора к нагрузке. Таким образом, коэффициенты A _U , A _I представляют собой комплексные амплитуды падающих волн напряжения и тока соответственно, а коэффициенты B _U , B _I — комплексные амплитуды отраженных волн напряжения и тока соответственно. Так как часть мощности, передаваемой по линии, может поглощаться в нагрузке, то амплитуды отраженных волн не должны превышать амплитуды падающих:

${\displaystyle |B_{U}|\leqslant |A_{U}|}$

${\displaystyle |B_{I}|\leqslant |A_{I}|}$

Направление распространения волн в (6) определяется знаком в показателях степени экспонент: плюс — волна распространяется в отрицательном направлении оси z ; минус — в положительном направлении оси z (см. рис. 1). Так, например, для падающих волн напряжения и тока можно записать:

${\displaystyle {\begin{cases}U_{\Pi }=A_{U}e^{-\gamma z}\\I_{\Pi }=A_{I}e^{-\gamma z}\\\end{cases}}}$ ,

(7)

Коэффициент распространения волны в линии γ в общем случае является комплексной величиной и может быть представлен в виде:

${\displaystyle \gamma ={\sqrt {Z_{1}Y_{1}}}={\sqrt {(R_{1}+i\omega L_{1})(G_{1}+i\omega C_{1})}}=\alpha +i\beta }$ ,

(8)

где α — коэффициент затухания волны в линии; β — коэффициент фазы . Тогда соотношение (7) можно переписать в виде:

${\displaystyle {\begin{cases}U_{\Pi }=A_{U}e^{-\alpha z}e^{-i\beta z}\\I_{\Pi }=A_{I}e^{-\alpha z}e^{-i\beta z}\\\end{cases}}}$ .

(9)

Так как при распространении падающей волны на длину волны в линии λ _Л фаза волны изменяется на 2 π , то коэффициент фазы можно связать с длиной волны λ _Л соотношением

${\displaystyle \beta ={\frac {2\pi }{\lambda _{\Lambda }}}}$ .

(10)

При этом фазовая скорость волны в линии V _Ф определяется через коэффициент фазы:

${\displaystyle V_{\Phi }={\frac {\omega }{\beta }}}$ .

(11)

Определим коэффициенты A и B , входящие в решения (6) волновых уравнений, через значения напряжения U _Н и тока I _Н на нагрузке. Это является оправданным, так как напряжение и ток на нагрузке практически всегда можно измерить с помощью измерительных приборов. Воспользуемся первым из телеграфных уравнений (2) и подставим в него напряжение и ток из (6). Тогда получим:

${\displaystyle A_{U}\gamma e^{-\gamma z}-B_{U}\gamma e^{\gamma z}=Z_{1}(A_{I}e^{-\gamma z}+B_{I}e^{\gamma z})}$

Сравнив коэффициенты при экспонентах с одинаковыми показателями степеней, получим:

${\displaystyle {\begin{cases}A_{I}={\frac {A_{U}}{W}}\\B_{I}=-{\frac {B_{U}}{W}}\\\end{cases}}}$ ,

(12)

где ${\displaystyle W={\sqrt {\frac {Z_{1}}{Y_{1}}}}}$ — волновое сопротивление линии .

Перепишем (6) с учётом (12):

${\displaystyle {\begin{cases}U=A_{U}e^{-\gamma z}+B_{U}e^{\gamma z}\\I={\frac {A_{U}e^{-\gamma z}-B_{U}e^{\gamma z}}{W}}\\\end{cases}}}$ .

(13)

Для определения коэффициентов A и B в этих уравнениях воспользуемся условиями в начале линии z = 0 :

${\displaystyle {\begin{cases}U(z=0)=U_{H}\\I(z=0)=I_{H}\\\end{cases}}}$ .

Тогда из (13) при z = 0 найдем

${\displaystyle {\begin{cases}A_{U}={\tfrac {1}{2}}(U_{H}+I_{H}W)\\B_{U}={\tfrac {1}{2}}(U_{H}-I_{H}W)\\\end{cases}}}$ ,

(14)

Подставив полученные значения коэффициентов из (14) в (13), после преобразований получим:

${\displaystyle {\begin{cases}U=U_{H}\operatorname {ch} (\gamma z)-I_{H}W\operatorname {sh} (\gamma z)\\I=I_{H}\operatorname {ch} (\gamma z)-{\frac {U_{H}}{W}}\operatorname {sh} (\gamma z)\\\end{cases}}}$ .

(15)

При выводе (15) учтены определения гиперболических синуса и косинуса .

Соотношения для напряжения и тока (15) так же, как и (6), являются решениями однородных волновых уравнений. Их отличие состоит в том, что напряжение и ток в линии в соотношении (6) определены через амплитуды падающей и отраженной волн, а в (15) — через напряжение и ток на нагрузке.

Рассмотрим простейший случай, когда напряжение и ток в линии определяются только падающей волной, а отраженная волна отсутствует . Тогда в (6) следует положить B _U = 0 , B _I = 0 :

${\displaystyle {\begin{cases}U=A_{U}e^{-\alpha z}e^{-i\beta z}\\I=A_{I}e^{-\alpha z}e^{-i\beta z}\\\end{cases}}}$ .

Распределение поля падающей волны

На рис.3. представлены эпюры изменения амплитуды | U | и фазы φ _U напряжения вдоль линии. Эпюры изменения амплитуды и фазы тока имеют такой же вид. Из рассмотрения эпюр следует, что при отсутствии в линии потерь ( α = 0 ) амплитуда напряжения в любом сечении линии остается одной и той же. При наличии потерь в линии ( α > 0 ) часть переносимой мощности преобразуется в тепло (нагревание проводов линии и окружающего их диэлектрика). По этой причине амплитуда напряжения падающей волны экспоненциально убывает в направлении распространения.

Фаза напряжения падающей волны φ _U = β z изменяется по линейному закону и уменьшается по мере удаления от генератора.

Рассмотрим изменение амплитуды и фазы, например, напряжения при наличии падающей и отраженной волн. Для упрощения положим, что потери в линии отсутствуют, то есть α = 0 . Тогда напряжение в линии можно представить в виде:

${\displaystyle U=A_{U}e^{-i\beta z}+B_{U}e^{i\beta z}=A_{U}(e^{-i\beta z}+\Gamma e^{i\beta z})}$ ,

(16)

где ${\displaystyle \Gamma =B_{U}/A_{U}}$ — комплексный коэффициент отражения по напряжению .

Комплексный коэффициент отражения по напряжению

Характеризует степень согласования линии передачи с нагрузкой. Модуль коэффициента отражения изменяется в пределах: ${\displaystyle 0\leqslant |\Gamma |\leqslant 1}$

• | Г | = 0 , если отражения от нагрузки отсутствуют и B _U = 0 ;
• | Г | = 1 , если волна полностью отражается от нагрузки, то есть ${\displaystyle |A_{U}|=|B_{U}|}$ ;

Соотношение (16) представляет собой сумму падающей и отраженной волн.

Отобразим напряжение на комплексной плоскости в виде векторной диаграммы, каждый из векторов которой определяет падающую, отраженную волны и результирующее напряжение (рис. 4). Из диаграммы видно, что существуют такие поперечные сечения линии, в которых падающая и отраженная волны складываются в фазе. Напряжение в этих сечениях достигает максимума, величина которого равна сумме амплитуд падающей и отраженной волн:

${\displaystyle U_{max}=|A_{U}|+|B_{U}|}$ .

Кроме того, существуют такие поперечные сечения линии, в которых падающая и отраженная волны складываются в противофазе. При этом напряжение достигает минимума:

${\displaystyle U_{min}=|A_{U}|-|B_{U}|}$ .

Если линия нагружена на сопротивление, для которого | Г | = 1 , то есть амплитуда падающей и отраженной волн равны | B _U | = | A _U | , то в этом случае U _max = 2| A _U | , а U _min = 0 .

Напряжение в такой линии изменяется от нуля до удвоенной амплитуды падающей волны. На рис. 5 представлены эпюры изменения амплитуды и фазы напряжения вдоль линии при наличии отраженной волны.

Коэффициенты бегущей и стоячей волны

По эпюре напряжения судят о степени согласования линии с нагрузкой. Для этого вводятся понятия коэффициента бегущей волны — k _БВ и коэффициента стоячей волны k _СВ :

${\displaystyle k_{bv}={\frac {U_{min}}{U_{max}}}={\frac {|A_{U}|-|B_{U}|}{|A_{U}|+|B_{U}|}}={\frac {1-|\Gamma |}{1+|\Gamma |}}}$	(17)
${\displaystyle k_{sv}={\frac {1}{k_{bv}}}}$	(18)

Эти коэффициенты, судя по определению, изменяются в пределах:

${\displaystyle 0\leqslant k_{bv}\leqslant 1}$ ,

${\displaystyle 1\leqslant k_{sv}\leqslant \infty }$ .

На практике наиболее часто используется понятие коэффициента стоячей волны, так как современные измерительные приборы (панорамные измерители k _СВ ) на индикаторных устройствах отображают изменение именно этой величины в определенной полосе частот.

Входное сопротивление длинной линии

Входное сопротивление линии является важной характеристикой, которое определяется в каждом сечении линии как отношение напряжения к току в этом сечении:

${\displaystyle Z_{BX}=R_{BX}+iX_{BX}}$
${\displaystyle Z_{BX}(z)={\frac {U(z)}{I(z)}}}$	(19)

Так как напряжение и ток в линии изменяются от сечения к сечению, то и входное сопротивление линии изменяется относительно её продольной координаты z . При этом говорят о трансформирующих свойствах линии, а саму линию рассматривают как трансформатор сопротивлений. Подробнее свойство линии трансформировать сопротивления будет рассмотрено ниже.

Режимы работы длинной линии

Различают три режима работы линии:

1. режим бегущей волны;
2. режим стоячей волны;
3. режим смешанных волн.

Режим бегущей волны

Режим бегущей волны характеризуется наличием только падающей волны, распространяющейся от генератора к нагрузке. Отраженная волна отсутствует. Мощность, переносимая падающей волной, полностью выделяется в нагрузке. В этом режиме B _U = 0 , | Г | = 0, k _св = k _бв = 1 .

Режим стоячей волны

Режим стоячей волны характеризуется тем, что амплитуда отраженной волны равна амплитуде падающей B _U = A _U то есть энергия падающей волны полностью отражается от нагрузки и возвращается обратно в генератор. В этом режиме, | Г | = 1 , k _св = ${\displaystyle \infty }$ , k _бв = 0 .

Режим смешанных волн

В режиме смешанных волн амплитуда отраженной волны удовлетворяет условию 0 < B _U < A _U то есть часть мощности падающей волны теряется в нагрузке, а остальная часть в виде отраженной волны возвращается обратно в генератор. При этом 0  < | Г | < 1 , 1 < k _св < ${\displaystyle \infty }$ , 0 < k _бв < 1

Линия без потерь

В линии без потерь погонные параметры R ₁ = 0 и G ₁ = 0 . Поэтому для коэффициента распространения γ и волнового сопротивления W получим:

${\displaystyle \gamma ={\sqrt {Z_{1}Y_{1}}}={\sqrt {(R_{1}+i\omega L_{1})(G_{1}+i\omega C_{1})}}=i\omega {\sqrt {L_{1}C_{1}}}}$ ; ${\displaystyle \alpha =0;~~\beta =\omega {\sqrt {L_{1}C_{1}}};~~W={\sqrt {\frac {Z_{1}}{Y_{1}}}}={\sqrt {\frac {L_{1}}{C_{1}}}}}$ .

(20)

С учётом этого выражения для напряжения и тока (15) примут вид:

${\displaystyle {\begin{matrix}U=U_{H}\cos(\beta z)&+&iI_{H}W\sin(\beta z)\\I=I_{H}\cos(\beta z)&+&i{\tfrac {U_{H}}{W}}\sin(\beta z)\end{matrix}}}$

(21)

При выводе этих соотношений учтены особенности гиперболических функций .

Рассмотрим конкретные примеры работы линии без потерь на простейшие нагрузки.

Разомкнутая линия

В этом случае ток, протекающий через нагрузку равен нулю ( I _Н = 0) , поэтому выражения для напряжения, тока и входного сопротивления в линии принимают вид:

${\displaystyle U=U_{H}\cos(\beta z);\quad I=i{\frac {U_{H}}{W}}\sin(\beta z)}$ ${\displaystyle Z_{BX}={\frac {U}{I}}=-iW\operatorname {ctg} (\beta z)=iX_{BX}}$ ${\displaystyle \beta ={\frac {2\pi }{\lambda }}}$

(22)

На рис.6 эти зависимости проиллюстрированы графически. Из соотношений (22) и графиков следует:

• в линии, разомкнутой на конце, устанавливается режим стоячей волны, напряжение, ток и входное сопротивление вдоль линии изменяются по периодическому закону с периодом λ _Л /2 ;
• входное сопротивление разомкнутой линии является чисто мнимым за исключением точек с координатами z = nλ _Л /4 , n = 0,1,2,… ;
• если длина разомкнутой линии меньше λ _Л /4 , то такая линия эквивалентна ёмкости;
• разомкнутая на конце линия длиной λ _Л /4 эквивалентна последовательному резонансному на рассматриваемой частоте контуру и имеет нулевое входное сопротивление;
• линия, длина которой лежит в интервале от λ _Л /4 до λ _Л /2 , эквивалентна индуктивности;
• разомкнутая на конце линия длиной λ _Л /2 эквивалентна параллельному резонансному контуру на рассматриваемой частоте и имеет бесконечно большое входное сопротивление.

Замкнутая линия

В этом случае напряжение на нагрузке равно нулю ( U _Н = 0) , поэтому напряжение, ток и входное сопротивление в линии принимают вид:

${\displaystyle U=iI_{H}W\sin(\beta z);\quad I=I_{H}\cos(\beta z)}$ ${\displaystyle Z_{BX}={\frac {U}{I}}=iW\operatorname {tg} (\beta z)=iX_{BX}}$

(23)

На рис.7 эти зависимости проиллюстрированы графически.

Используя результаты предыдущего раздела, нетрудно самостоятельно сделать выводы о трансформирующих свойствах короткозамкнутой линии. Отметим лишь, что в замкнутой линии также устанавливается режим стоячей волны. Отрезок короткозамкнутой линии, длиной меньше λ _Л /4 имеет индуктивный характер входного сопротивления, а при длине λ _Л /4 такая линия имеет бесконечно большое входное сопротивление на рабочей частоте .

Ёмкостная нагрузка

Как следует из анализа работы разомкнутой линии, каждой ёмкости C на данной частоте ω можно поставить в соответствие отрезок разомкнутой линии длиной меньше λ _Л /4 . Ёмкость C имеет ёмкостное сопротивление ${\displaystyle iX_{C}=-{\tfrac {i}{\omega C}}}$ . Приравняем величину этого сопротивления к входному сопротивлению разомкнутой линии длиной l < λ _Л /4 :

${\displaystyle -{\tfrac {i}{\omega C}}=-iW\operatorname {ctg} (\beta l)}$ .

Отсюда находим длину линии, эквивалентную по входному сопротивлению ёмкости C :

${\displaystyle l={\tfrac {1}{\beta }}\operatorname {arctg} (\omega CW)}$ .

Зная эпюры напряжения, тока и входного сопротивления разомкнутой линии, восстанавливаем их для линии, работающей на ёмкость (рис.8). Из эпюр следует, что в линии, работающей на ёмкость, устанавливается режим стоячей волны.

При изменений ёмкости эпюры сдвигаются вдоль оси z . В частности, при увеличении ёмкости ёмкостное сопротивление уменьшается, напряжение на ёмкости падает и все эпюры сдвигаются вправо, приближаясь к эпюрам, соответствующим короткозамкнутой линии. При уменьшении ёмкости эпюры сдвигаются влево, приближаясь к эпюрам, соответствующим разомкнутой линии.

Индуктивная нагрузка

Как следует из анализа работы замкнутой линии, каждой индуктивности L на данной частоте ω можно поставить в соответствие отрезок замкнутой линии длиной меньше λ _Л /4 . Индуктивность L имеет индуктивное сопротивление iX _Л = iωL . Приравняем это сопротивление к входному сопротивлению замкнутой линии длиной λ _Л /4 :

${\displaystyle i\omega L=iW\operatorname {tg} (\beta l)}$ .

Отсюда находим длину линии l , эквивалентную по входному сопротивлению индуктивности L :

${\displaystyle l={\tfrac {1}{\beta }}\operatorname {arctg} (\omega {\tfrac {L}{W}})}$ .

Зная эпюры напряжения, тока и входного сопротивления замкнутой на конце линии, восстанавливаем их для линии, работающей на индуктивность (рис. 9). Из эпюр следует, что в линии, работающей на индуктивность, также устанавливается режим стоячей волны. Изменение индуктивности приводит к сдвигу эпюр вдоль оси z . Причем с увеличением L эпюры сдвигаются вправо, приближаясь к эпюрам холостого хода, а с уменьшением L — влево по оси z , стремясь к эпюрам короткого замыкания.

Активная нагрузка

В этом случае ток и напряжение на нагрузке R _Н связаны соотношением U _Н = I _Н R _Н . Выражения для напряжения и тока в линии (21) принимают вид:

${\displaystyle U=U_{H}\cos(\beta z)+iU_{H}{\tfrac {W}{R_{H}}}\sin(\beta z)}$ ${\displaystyle I=I_{H}\cos(\beta z)+iI_{H}{\tfrac {R_{H}}{W}}\sin(\beta z)}$

(23)

Рассмотрим работу такой линии на примере анализа напряжения. Найдем из (23) амплитуду напряжения в линии:

${\displaystyle |U|=U_{H}{\sqrt {\cos ^{2}(\beta z)+\left({\tfrac {W}{R_{H}}}\right)^{2}\sin ^{2}(\beta z)}}}$

(24)

Отсюда следует, что можно выделить три случая:

• Сопротивление нагрузки равно волновому сопротивлению линии R _Н = W ;
• Сопротивление нагрузки больше волнового сопротивления линии R _Н > W;
• Сопротивление нагрузки меньше волнового сопротивления линии R _Н < W.

В первом случае из (24) следует | U | = U _Н , то есть распределение амплитуды напряжения вдоль линии остается постоянным, равным амплитуде напряжения на нагрузке. Это соответствует режиму бегущей волны в линии.

Комплексная нагрузка

КПД линии с потерями

Пределы применимости теории длинной линии

См. также

• Измерительная линия
• Металлический изолятор
• Диаграмма Вольперта — Смита

Примечания