Морвен Бернард Тистлетвэйт ( англ. Morwen Bernard Thistlethwaite ; род. 1942 ) — британский математик, теоретик в области теории узлов и теории групп . Профессор математики университета Теннесси в Ноксвилле . Внёс большой вклад в теорию узлов и теорию группы кубика Рубика .

Биография

Морвен Тистлетвэйт получил степень бакалавра искусств в Кембриджском университете в 1967, магистра в Лондонском университете в 1968 и PhD (доктора философии) в Манчестерском университете в 1972, где его научным руководителем был Майкл Барат. Он учился игре на фортепиано с Таней Полуниной, Джеймсом Гиббом и и давал концерты в Лондоне, прежде чем решил посвятить себя карьере математика в 1975. Он учился в с 1975 по 1978 и в с 1978 по 1987. Он работал в качестве внештатного профессора в Калифорнийском университета в Санта-Барбаре около года, прежде чем перешёл в Университет в Теннесси , в котором он по настоящее время является профессором. В 2022 года Тистлтуэйт был принят действительным членом Американского математического общества «за вклад в топологию низких размерностей, особенно за разрешение гипотез классической теории узлов Тейта и за табулирование узлов» . Сын Тистлетвэйта также математик .

Работа

Гипотезы Тэйта

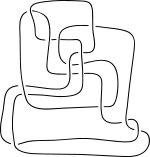
Морвен Тистлетвэйт помог доказать гипотезы Тэйта

1. Приведённые альтернированные диаграммы имеют минимальное число пересечений .
2. Любые две приведенные альтернированные диаграммы заданного узла имеют одинаковое число закрученности .
3. Если даны любые две приведенные альтернированные диаграммы D ₁ и D ₂ ориентированного простого альтернированного зацепления D ₁ может быть преобразована в D ₂ путём последовательности простых движений, называемых . Гипотеза известна как .
   (адаптирован из MathWorld—A Wolfram Web Resource. )

Морвен Тистлетвэйт вместе с и доказал первые две гипотезы Тэйта в 1987. Тистлетвэйт и доказали в 1991.

Алгоритм Тистлетвэйта

Тистлетвэйт знаменит также благодаря его алгоритму сборки кубика Рубика . Алгоритм разбивает состояния кубика Рубика на группы , которые можно получить с помощью определённых ходов. Вот эти группы:

• G ₀ = <L,R,F,B,U,D>

Эта группа содержит все позиции кубика Рубика.

• G ₁ = <L,R,F,B,U2,D2>

Эта группа содержит все позиции, которые могут быть достигнуты (с собранного состояния) с помощью вращения на одну четвёртую левой, правой, передней и задней сторон кубика Рубика, но только вращений на пол-оборота верхней и нижней сторон.

• G ₂ = <L,R,F2,B2,U2,D2>

В этой группе состояния ограничены теми, которые можно получить вращением на пол-оборота передней, задней верхней и нижней сторон кубика и на одну четверть левой и правой граней.

• G ₃ = <L2,R2,F2,B2,U2,D2>

Состояния этой группы могут быть получены только вращением в пол-оборота всех граней.

• G ₄ = {I}

Финальная группа содержит только одно состояние — собранный кубик.

Кубик собирается путём движения от группы к группе с помощью ходов, разрешённых для данной группы. Например, перемешанный кубик, скорее всего, находится в состоянии G ₀ . Просматривается таблица возможных перестановок, которые используют вращения на одну четверть, чтобы перевести кубик в группу G ₁ . Теперь вращения на одну четверть верхней и нижней грани запрещаются в последовательностях в таблице и используются вращения из таблицы для получения состояния G ₂ . И так далее, пока кубик не будет собран.

Нотация Даукера-Тистлетвэйта

Тистлетвэйт вместе с разработали , обозначение узлов , пригодное для использования в компьютерах и являющееся производным от нотаций Тэйта и Гаусса .

См. также

• Математика кубика Рубика

Примечания

Литература

Ссылки

• — Morwen Thistlethwaite's home page.
• (англ.) в проекте « Математическая генеалогия »