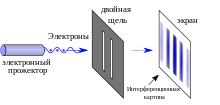
Двухщелево́й опыт в (англ.) ( является демонстрацией того, что свет и материя в целом могут проявлять характеристики как классических волн, так и частиц; кроме того, он отображает фундаментально вероятностный характер квантово-механических явлений. Впервые опыт был проведён Томасом Юнгом со светом в 1801 году. В 1927 году Дэвиссон и Гермер продемонстрировали, что электроны проявляют такое же поведение, которое позднее расширено на атомы и молекулы.

Опыт Томаса Юнга со светом был частью классической физики задолго до квантовой механики и концепции корпускулярно-волнового дуализма . Он полагал, что это продемонстрировало правильность волновой теории света . Его опыт иногда называют «щели Юнга».

Этот опыт относится к общему классу опытов с «двойным путём», в которых первоначальная волна разделяется на две раздельные, которые впоследствии снова объединяются в одну. Изменения длины пути обеих волн приводят к сдвигу фаз , создавая интерференционную картину . Другой версией опыта является интерферометр Маха — Цендера , который разделяет луч при помощи зеркала.

Квантовая механика
История Математические основы
Основа Классическая механика Постоянная Планка Интерференция Бра и кет Гамильтониан Старая квантовая теория
Фундаментальные понятия Квантовое состояние Квантовая наблюдаемая Волновая функция Квантовая суперпозиция Квантовая запутанность Смешанное состояние Измерение Неопределённость Принцип Паули Дуализм Декогеренция Симметрия Теорема Эренфеста Туннельный эффект
Эксперименты Опыт Дэвиссона — Джермера Опыт Франка — Герца Опыт Штерна — Герлаха Опыт Юнга Квантовый ластик Квантовый ластик с отложенным выбором Проверка неравенств Белла Фотоэффект Эффект Комптона
Формулировки Представление Шрёдингера Представление Гейзенберга Представление взаимодействия Представление фазового пространства Матричная квантовая механика Интегралы по траекториям Диаграммы Фейнмана
Уравнения Шрёдингера Паули Клейна — Гордона Дирака Швингера — Томонаги фон Неймана Блоха Линдблада Гейзенберга
Интерпретации Копенгагенская Теория скрытых параметров Супердетерминизм Многомировая Теория де Бройля — Бома
Развитие теории Квантовая теория поля Квантовая электродинамика Теория Глэшоу — Вайнберга — Салама Квантовая хромодинамика Стандартная модель Квантовая гравитация
Сложные темы Релятивистская квантовая механика Квантовая теория поля Квантовая гравитация Теория всего
Известные учёные Планк Эйнштейн Шрёдингер Гейзенберг Йордан Бор Паули Дирак Фок Борн де Бройль Ландау Фейнман Бом Эверетт
См. также История возникновения ЭПР-парадокс
См. также: Портал:Физика

В базовой версии этого опыта источник когерентного света, такой как лазерный луч, освещает пластину с двумя параллельными щелями, и свет, проходящий через щели, наблюдают на экране за пластиной. Волновая природа света вызывает интерференцию световых волн, проходящих через две щели, создавая яркие и тёмные полосы на экране — результат, которого не должно было бы быть, если бы свет состоял из классических частиц. Однако всегда обнаруживается, что свет поглощается на экране в отдельных точках, в виде отдельных частиц (не волн), а интерференционная картина появляется из-за изменяющейся плотности попадания этих частиц на экран. Кроме того, версии опыта, включающие детекторы в щелях, обнаруживают, что каждый обнаруженный фотон проходит только через одну щель (как классическая частица), а не через обе щели (как волна). Тем не менее, такие опыты показывают, что частицы не образуют интерференционную картину, если наблюдать, через какую щель они проходят. Эти результаты демонстрируют принцип корпускулярно-волнового дуализма .

Обнаружено, что другие объекты атомного масштаба, например электроны , проявляют то же поведение при стрельбе по двойной щели. Кроме того, наблюдение отдельных дискретных взаимодействий по своей природе является вероятностным, что необъяснимо с помощью классической механики .

Опыт может быть сделан с намного более крупными объектами, чем электроны и фотоны, хотя он становится более сложным с увеличением размеров. Крупнейшими объектами, для которых был проведён опыт с двумя щелями, были молекулы , каждая из которых содержала 810 атомов (общая масса которых составляла более 10000 атомных единиц массы ).

Двухщелевой опыт (и его вариации) стал классическим мысленным экспериментом , как яркий пример загадок квантовой механики. Поскольку он демонстрирует фундаментальное ограничение способности наблюдателя прогнозировать экспериментальные результаты, Ричард Фейнман назвал это «явлением, которое невозможно […] объяснить каким-либо классическим способом , и в котором заложено сердце квантовой механики. В действительности, оно содержит единственную тайну [квантовой механики]» .

Обзор

Если бы свет состоял строго из обычных или классических частиц, и эти частицы выпускались бы по прямой линии через щель, что позволяло бы им попадать в экран на другой стороне, мы ожидали бы увидеть изображение, соответствующее размеру и форме щели. Однако, когда этот «эксперимент с одной щелью» выполняется в реальности, изображение на экране представляет собой дифракционную картину распределения света. Чем меньше щель, тем больше угол расхождения. В верхней части изображения показана центральная часть паттерна, сформированного при освещении лазером щели. Также можно заметить две слабые боковые полосы. Большее число полос можно увидеть с более точной установкой. Изображение объясняется дифракцией как результат интерференции световых волн от щели.

Если освещать две параллельные щели, то свет от двух щелей дополнительно интерферирует. Здесь интерференция представляет собой более выраженный паттерн с чередованием светлых и тёмных полос. Ширина полос зависит от частоты испускаемого света . (См. нижнюю фотографию справа.) Когда Томас Юнг (1773—1829) впервые продемонстрировал это явление, он указал, что свет состоит из волн, поскольку распределение яркости может быть объяснено попеременно аддитивной и вычитающей интерференцией волнового фронта . Опыт Юнга , выполненный в начале 1800-х годов, сыграл критически важную роль в принятии волновой теории света, победив корпускулярную теорию света , предложенную Исааком Ньютоном , которая была принятой моделью распространения света в 17-м и 18-м веках. Однако позднее обнаружение фотоэлектрического эффекта продемонстрировало, что при различных обстоятельствах свет может вести себя так, как если бы он состоял из дискретных частиц. Эти, казалось бы, противоречивые открытия заставили выйти за рамки классической физики и принять во внимание квантовую природу света.

Фейнман любил говорить, что всю квантовую механику можно получить из тщательного обдумывания последствий этого единственного эксперимента . Он также предложил (в качестве мысленного эксперимента), что размещение детекторов перед каждой щелью приведёт к исчезновению интерференционной картины .

Соотношение (англ.) ( подробно описывает математику двухщелевой интерференции в контексте квантовой механики.

Низкоинтенсивный двухщелевой опыт был впервые выполнен Дж. И. Тейлором в 1909 г. путём снижения уровня падающего света до тех пор, пока события испускания/поглощения фотонов большей частью не перекрывались. Двухщелевой опыт не проводился ни с чем, кроме света, до 1961 года, когда из Тюбингенского университета выполнил его с электронными пучками . В 1974 году итальянские физики Пьер Джорджо Мерли, Джан Франко Миссироли и повторили опыт, используя одиночные электроны и бипризму (вместо щелей), показав, что каждый электрон взаимодействует с самим собой, как и предсказывает квантовая теория . В 2002 году одноэлектронная версия опыта была признана читателями журнала Physics World «самым красивым экспериментом» .

В 2012 году Стефано Фраббони и его коллеги в конечном итоге провели двухщелевой опыт с электронами и реальными щелями, следуя оригинальной схеме, предложенной Фейнманом. Они посылали одиночные электроны на нанофабрикатные щели (шириной около 100 нм) и, собирая прошедшие электроны одноэлектронным детектором, смогли показать накопление двухщелевой интерференционной картины .

В 2019 году Марко Джаммарки и его коллеги продемонстрировали интерференцию отдельных частиц для антиматерии .

Варианты опыта

Интерференция отдельных частиц

Важная версия этого эксперимента подразумевает одиночные частицы (или волны — для согласованности они называются здесь частицами). Испускание одиночных частиц через устройство с двумя щелями приводит к ожидаемому появлению на экране одиночных частиц. Примечательно, однако, что интерференционная картина возникает, если эти частицы накапливать (см. соседнее изображение). Это демонстрирует корпускулярно-волновой дуализм , который утверждает, что вся материя проявляет свойства как волн, так и частиц: частица измеряется как один импульс в одной позиции, а волна описывает вероятность поглощения частицы в определённом месте на экране. Было показано, что это явление происходит с фотонами, электронами, атомами и даже некоторыми молекулами, включая букибол . Таким образом, эксперименты с электронами добавляют подтверждающее доказательство к мнению, что электроны, протоны, нейтроны и даже более крупные объекты, которые обычно называют частицами, тем не менее, имеют свою собственную волновую природу и даже длину волны (связанную с их импульсом).

Вероятность обнаружения является квадратом амплитуды волны и может быть рассчитана с помощью классических волн (см. ниже). Частицы не попадают на экран в определённом порядке, поэтому знание того, где появились на экране и в каком порядке все предыдущие частицы, ничего не говорит о том, где будет обнаружена следующая частица. Если в каком-то месте происходит затухание волн, это не означает исчезновение частицы; она появится где-то в другом месте. С момента появления квантовой механики некоторые теоретики искали способы включения дополнительных детерминант или « скрытых параметров », зная которые было бы возможно определять местоположение каждого отдельного попадания в мишень.

Более сложные системы, которые включают две и более частиц в суперпозиции, приведённому выше объяснению не поддаются.

Интерферометр Маха — Цендера

Интерферометр Маха — Цендера можно рассматривать как упрощённую версию эксперимента с двумя щелями. Вместо того, чтобы распространяться через свободное пространство после двух щелей и попадать в любую точку широкого экрана, в интерферометре фотоны могут распространяться только по двум путям и попадать в два дискретных фотодетектора. Это позволяет описывать процесс с помощью простой линейной алгебры размерности 2 вместо дифференциальных уравнений.

Фотон, испускаемый лазером, попадает в первый светоделитель и затем оказывается в суперпозиции между двумя возможными траекториями. Во втором светоделителе эти пути интерферируют, в результате чего фотон попадает в фотодетектор справа с вероятностью один и в фотодетектор внизу с вероятностью ноль. Интересно, что если фотон оказывается только на одном из путей между светоделителями, этого можно достичь, заблокировав один из путей, или, что то же самое, пронаблюдав там присутствие фотона, то в обоих случаях интерференция пропадает, и оба фотодетектора будут срабатывать с вероятностью 1/2. Из этого факта мы можем заключить, что фотон не идёт по одному из путей после первого светоделителя, а скорее находится в настоящей квантовой суперпозиции двух путей.

Опыты по выявлению пути и принцип дополнительности

Известный мысленный эксперимент предсказывает, что если детекторы частиц будут расположены на щелях, показывая, через какую щель проходит фотон, интерференционная картина исчезнет . Этот опыт по выявлению пути иллюстрирует принцип дополнительности , согласно которому фотоны могут вести себя как частицы или волны, но не могут одновременно наблюдаться в обоих вариантах. Несмотря на важность этого мысленного эксперимента в истории квантовой механики (например, см. обсуждение версии этого эксперимента Эйнштейном ), технически осуществимые реализации этого эксперимента не существовали до 1970-х годов. (Наивные реализации хрестоматийного мысленного эксперимента невозможны, поскольку фотоны не могут быть обнаружены без поглощения фотона.) В настоящее время было проведено несколько экспериментов, иллюстрирующих различные аспекты дополнимости.

Эксперимент, проведённый в 1987 году дал результаты, которые продемонстрировали, что можно получить информацию о том, по какому пути прошла частица, вообще не разрушая интерференцию. Это продемонстрировало эффект измерения, которое слабо воздействовало на летящие частицы и тем самым сопоставимо влияло на интерференционную картину. Другими словами, если не настаивать на полностью надёжном методе, используемом для определения щели, через которую проходит каждый фотон, по прежнему наблюдается (ухудшенная) интерференционная картина.

Отложенный выбор и варианты квантового ластика

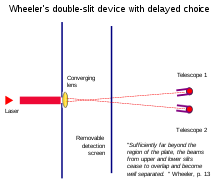
(англ.) ( демонстрируют, что извлечение информации о пути после того, как частица прошла через щели, может, как кажется, задним числом поменять предшествующее поведение на щелях.

Эксперимент квантового ластика демонстрирует, что волновое поведение может быть восстановлено путём стирания информации о пути.

Простая «домашняя» иллюстрация «квантового ластика» была дана в статье в журнале Scientific American . Если установить поляризаторы перед каждой щелью так, чтобы их оси были ортогональны друг другу, интерференционная картина пропадёт. Поляризаторы могут рассматриваться как добавляющие к каждому лучу информацию о пути. Введение третьего поляризатора перед детектором с осью 45° относительно других поляризаторов, «стирает» эту информацию, восстанавливая интерференционную картину. Это также можно объяснить, рассматривая свет как классическую волну ^:91 а также при использовании круговых поляризаторов и одиночных фотонов. ^:6 Реализации поляризаторов с использованием запутанных фотонных пар не имеют классического объяснения .

Слабое измерение

В широко разрекламированном эксперименте 2012 года исследователи утверждали, что определили путь, по которому прошла каждая частица, без какого-либо отрицательного воздействия на интерференционную картину. Для этого они использовали установку, где частицы вылетали не из точечного источника, а из источника с двумя максимумами интенсивности. Однако такие комментаторы, как Свенссон , отметили, что на самом деле нет никакого конфликта между слабыми измерениями , выполненными в этом варианте двухщелевого эксперимента, и принципом неопределённости Гейзенберга . Слабое измерение с последующим выбором не позволяло одновременно измерять положение и импульс для каждой отдельной частицы, а скорее позволяло измерять среднюю траекторию частиц, которые попали в разные позиции. Другими словами, экспериментаторы создавали статистическую карту ландшафта полной траектории.

Другие варианты

В 1967 году Пфлегор и Мандель продемонстрировали интерференцию с двумя источниками, используя два отдельных лазера в качестве источников света.

В 1972 году экспериментально было показано, что в двухщелевой системе, в которой была открыта только одна щель, также наблюдалась интерференция при условии разности путей, позволяющей детектируемому фотону приходить из любой щели. Плотность фотонов в экспериментальной системе была значительно меньше единицы.

В 1999 году эксперимент с двумя щелями был успешно проведён с молекулами букибола (каждая из которых содержит 60 атомов углерода) . Букибол достаточно большой (диаметр около 0,7 нм , почти в полмиллиона раз больше, чем протон), что позволяет наблюдать его под электронным микроскопом .

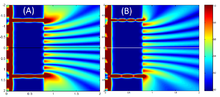
В 2005 году Э. Р. Элиель представил экспериментальное и теоретическое исследование оптического пропускания тонкого металлического экрана, с двумя щелями размерами менее длины волны, разделёнными расстоянием, превышающим длину волны во много раз. Показано, что общая интенсивность паттерна двойной щели в дальней зоне уменьшается или увеличивается как функция длины волны падающего светового пучка.

В 2012 году исследователи из Университета штата Небраска-Линкольн выполнили двухщелевой эксперимент с электронами, как описано Ричардом Фейнманом , с использованием новых инструментов, которые позволили контролировать проход двух щелей и отслеживать события обнаружения единичных электронов. Электроны запускались электронной пушкой и проходили через одну или две щели 62нм шириной и 4мкм высотой.

В 2013 году двухщелевой опыт был успешно проведён с молекулами, каждая из которых содержала 810 атомов (общая масса которых превышала 10000 атомных единиц массы ).

Гидродинамические аналоги волны-пилота

Были разработаны (англ.) ( , которые могут воссоздать различные аспекты квантово-механических систем, включая одночастичную интерференцию через двойную щель. Капля силиконового масла, отскакивая вдоль поверхности жидкости, самостоятельно движется посредством резонансных взаимодействий с собственным волновым полем. Капля мягко выплёскивает жидкость при каждом скачке. В то же время на её ход влияет рябь от прошлых отскоков. Взаимодействие капли с её собственной рябью, которая образует так называемую пилот-волну , приводит к тому, что капля демонстрирует поведение, ранее считавшееся характерным для элементарных частиц, — в том числе поведение, обычно принимаемое в качестве доказательства того, что элементарные частицы распространяются в пространстве, как волны, без какого-либо конкретное местоположения, до измерения.

Поведения, имитируемые с помощью такой гидродинамической системы пилот-волн, включают в себя квантовую одночастичную дифракцию, туннелирование, квантованные орбиты, расщепление орбитальных уровней, спин и мультимодальную статистику. Также можно вывести соотношение неопределённостей и принципы запрета. Имеются видеоролики, иллюстрирующие различные свойства такой системы.

Тем не менее, более сложные системы, которые включают суперпозицию двух и более частиц, не поддаются такому простому, классически интуитивному объяснению. Соответственно, не существует гидродинамического аналога квантовой запутанности. Тем не менее, возможны оптические аналоги.

Классическая волновая оптика

Большая часть поведения света может быть смоделирована с использованием классической волновой теории. Принцип Гюйгенса — Френеля является одной из таких моделей; в нём говорится, что каждая точка волнового фронта генерирует вторичную волну, и что возмущение в любой последующей точке можно найти, суммируя вклады отдельных волн в этой точке. Это суммирование должно учитывать фазу и амплитуду отдельных волн. Измерена может быть только интенсивность светового поля, которая пропорциональна квадрату амплитуды.

В двухщелевом опыте обе щели освещаются одним лазерным лучом. Если ширина щелей достаточно мала (меньше длины волны лазерного излучения), щели рассеивают свет на цилиндрические волны. Эти два цилиндрических волновых фронта накладываются друг на друга, и амплитуда и, следовательно, интенсивность в любой точке комбинированных волновых фронтов зависят как от величины, так и от фазы двух волновых фронтов. Разница в фазе между двумя волнами определяется разницей в расстоянии, пройденном этими волнами.

Если расстояние наблюдения велико по сравнению с разнесением щелей ( (англ.) ( ), разность фаз можно найти с помощью геометрии, показанной на нижнем правом рисунке. Разница в пути между двумя волнами, проходящими под углом θ , определяется как:

${\displaystyle d\sin \theta \approx d\theta }$

Где d — расстояние между двумя щелями. Когда две волны находятся в фазе, то есть разность путей равна целому числу длин волн, суммарная амплитуда и, следовательно, суммарная интенсивность максимальны, а когда они находятся в противофазе, то есть разность путей равна половине длина волны, полторы длины волны и т. д., то волны вычитаются и суммарная интенсивность равна нулю. Этот эффект известен как интерференция . Максимумы интерференционных полос возникают под углами

${\displaystyle ~d\theta _{n}=n\lambda ,~n=0,1,2,\ldots }$

где λ — длина волны света. Угловое расстояние между полосами, θ _f задаются как

${\displaystyle \theta _{f}\approx \lambda /d}$

Расстояние между полосами на расстоянии z от щелей определяется как

${\displaystyle ~w=z\theta _{f}=z\lambda /d}$

Например, если две щели разделены на 0,5 мм (d) и освещены лазером с длиной волны 0,6 мкм (λ), то на расстоянии 1м (z) расстояние между полосами составит 1,2 мм.

Если ширина щелей b больше длины волны, уравнение дифракции Фраунгофера даёт интенсивность дифрагированного света как:

${\displaystyle {\begin{aligned}I(\theta )&\propto \cos ^{2}\left[{\frac {\pi d\sin \theta }{\lambda }}\right]~\mathrm {sinc} ^{2}\left[{\frac {\pi b\sin \theta }{\lambda }}\right]\end{aligned}}}$

Где функция sinc определяется как sinc( x ) = sin( x )/ x для x ≠ 0 и sinc(0) = 1.

Это показано на рисунке выше, где первый узор представляет собой дифракционную картину от одной щели, заданную функцией sinc в этом уравнении, а второй рисунок показывает суммарную интенсивность света, дифрагированного от двух щелей, где функция cos формирует тонкую структуру, а более грубая структура формирует дифракцию от отдельных щелей, согласно функции sinc.

Аналогичные вычисления для (англ.) ( могут быть выполнены с использованием уравнения дифракции Френеля . По мере того, как плоскость наблюдения становится ближе к плоскости щелей, связанные с каждой щелью дифракционные картины уменьшаются в размерах, так что площадь интерференции уменьшается и может вообще исчезнуть, если нет перекрытия двух дифракционных картин.

Интерпретации эксперимента

Как и мысленный эксперимент с котом Шрёдингера , двухщелевой опыт часто используется для демонстрации различий и сходств между разными интерпретациями квантовой механики .

Копенгагенская интерпретация

Копенгагенская интерпретация , выдвинутая некоторыми пионерами в области квантовой механики, утверждает, что нежелательно постулировать что-либо, выходящее за рамки математических формул, физической аппаратуры и результатов, которые позволяют нам получить некоторые знания о том, что происходит на атомном уровне. Одну из математических конструкций, которая позволяет экспериментаторам очень точно прогнозировать определённые экспериментальные результаты, иногда называют «волной вероятности». По своей математической форме она аналогична описанию физической волны, но её «волны» и «гребни» указывают уровни вероятности возникновения определённых явлений (например, вспышки света в определённой точке на экране детектора), которые можно наблюдать в макромире повседневного опыта.

Можно сказать, что «волна» вероятности проходит через пространство, потому что значения вероятности, которые можно вычислить из её математического представления, зависят от времени. Нельзя говорить о местонахождении какой-либо частицы, такой как фотон, между моментами испускания и обнаружения, просто потому, что для утверждения о нахождении объекта в определённом месте в определённое время, нужно его обнаружить (детектировать). Требование возможного появления интерференционной картины состоит в том, что должны быть испускаемые частицы и экран с, по меньшей мере, двумя различными путями, по которым частица должна пройти от излучателя к экрану. В экспериментах нет наблюдения в промежуток времени между испусканием частицы и её попаданием в экран. Если произвести трассировку лучей так, как будто световая волна (как понимается в классической физике) достаточно широка для прохождения обоих путей, то эта трассировка будет точно предсказывать появление максимумов и минимумов на экране детектора, когда многие частицы проходят через аппарат и постепенно «раскрашивают» ожидаемую интерференционную картину.

Формулировка через интегралы по траекториям

Копенгагенская интерпретация аналогична формулировке квантовой механики через интегралы по траекториям, предложенной Фейнманом. Формула интеграла по траекториям заменяет классическое понятие единственной уникальной траектории для системы суммой по всем возможным траекториям. Траектории складываются вместе с помощью функционального интеграла .

Каждый путь считается одинаково вероятным и, следовательно, вносит одинаковый вклад. Однако фаза этого вклада в любой заданной точке пути определяется действием на пути:

${\displaystyle A_{\text{path}}(x,y,z,t)=e^{iS(x,y,z,t)}}$

Все эти вклады затем складываются, и величина конечного результата возводится в квадрат , чтобы получить распределение вероятностей для положения частицы:

${\displaystyle p(x,y,z,t)\propto \left\vert \int _{\text{all paths}}e^{iS(x,y,z,t)}\right\vert ^{2}}$

Как всегда при расчёте вероятности , результаты должны быть (англ.) ( путём наложения:

${\displaystyle \iiint _{\text{all space}}p(x,y,z,t)\,\mathrm {d} V=1}$

Подводя итог, можно сказать, что распределение вероятностей исхода — это нормализованный квадрат нормы суперпозиции по всем путям от точки происхождения до конечной точки волн, (англ.) ( пропорционально действию вдоль каждого пути. Различия в кумулятивном действии вдоль различных путей (и, следовательно, относительных фаз вкладов) создают интерференционную картину, наблюдаемую в двухщелевом опыте. Фейнман подчеркнул, что его формулировка является просто математическим описанием, а не попыткой описать реальный измеряемый процесс.

Реляционная интерпретация

Согласно реляционной интерпретации квантовой механики , впервые предложенной Карло Ровелли , наблюдения, подобные наблюдениям в двухщелевом опыте, являются результатом взаимодействия (англ.) ( (измерительного устройства) и наблюдаемого объекта (с которым физически взаимодействуют), а не какого-либо абсолютного свойства объекта. В случае электрона, если он изначально «наблюдается» на определённой щели, то взаимодействие наблюдатель-частица (фотон-электрон) включает информацию о положении электрона. Это частично ограничивает конечное местоположение частицы на экране. Если он «наблюдается» (измеряется с помощью фотона) не на конкретной щели, а на экране, то информация о пути не является частью взаимодействия, поэтому «наблюдаемое» положение электрона на экране определяется строго его вероятностной функции. Это делает результирующее изображение на экране таким же, как если бы каждый отдельный электрон прошёл через обе щели. Также было высказано предположение, что пространство и расстояние сами по себе являются реляционными, и что электрон может оказаться в «двух местах одновременно» — например, на обеих щелях — потому что его пространственные отношения с конкретными точками на экране остаются идентичными с положений щелей .

Многомировая интерпретация

Физик Дэвид Дойч утверждает в своей книге Структура реальности , что двухщелевой эксперимент является доказательством многомировой интерпретации . Однако, поскольку любая интерпретация квантовой механики эмпирически неразличима, некоторые учёные скептически относятся к этому утверждению.

Теория де Бройля — Бома

Альтернатива общепринятому пониманию квантовой механики, теория де Бройля — Бома утверждает, что частицы всегда имеют точное местоположение и что их скорости зависят от волновой функции. Таким образом, в то время как отдельная частица пройдёт через одну конкретную щель в двухщелевом опыте, так называемая «пилотная волна», которая влияет на неё, пройдёт через обе. Траектории двойной щели де Бройля-Бома были впервые рассчитаны Крисом Дьюдни во время работы с Крисом Филиппидисом и Бэзилом Хили в Биркбек-колледже (Лондон). Теория де Бройля-Бома даёт те же статистические результаты, что и стандартная квантовая механика, но обходится без многих её концептуальных трудностей.

См. также

Примечания

Ссылки

Интерактивные анимации

Эксперименты с одной частицей

Гидродинамический аналог

Компьютерное моделирование