Дифра́кция Френе́ля — дифракционная картина , которая наблюдается на небольшом расстоянии от препятствия, по условиям, когда основной вклад в интерференционную картину дают границы экрана.

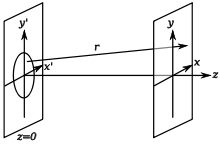
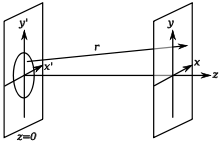
На рисунке схематично изображён (слева) непрозрачный экран с круглым отверстием ( апертура ), слева от которого расположен источник света . Изображение фиксируется на другом экране — справа. Вследствие дифракции свет, проходящий через отверстие, расходится, поэтому область, которая была затемнена по законам геометрической оптики , будет частично освещённой . В области, которая при прямолинейном распространении света была бы освещённой, наблюдаются колебания интенсивности освещения в виде концентрических колец.

Дифракционная картина для дифракции Френеля зависит от расстояния между экранами и от расположения источников света. Её можно рассчитать, считая, что каждая точка на границе апертуры излучает сферическую волну по принципу Гюйгенса . В точках наблюдения, на втором экране, волны или усиливают друг друга, или гасятся в зависимости от .

Интеграл Френеля

В скалярной теории дифракции распределение электрического поля дифрагирующего света в точке (x,y,z) задаётся выражением Релея-Зоммерфельда:

${\displaystyle E(x,y,z)=-{i \over \lambda }\iint _{-\infty }^{+\infty }{E(x',y',0){\frac {e^{ikr}}{r}}\cos \theta }dx'dy'}$

где ${\displaystyle r={\sqrt {(x-x')^{2}+(y-y')^{2}+z^{2}}}}$ , ${\displaystyle i}$ — мнимая единица , и ${\displaystyle \cos \theta ={\frac {z}{r}}}$ — косинус угла между направлениями z и r . В аналитическом виде этот интеграл представим только для простейших геометрий отверстий, поэтому он вычисляется обычно численными методами.

Аппроксимация Френеля

Главная трудность при вычислении интеграла представляет собой выражение для r . Во-первых, упростим вычисления, сделав замену переменных:

${\displaystyle \rho ^{2}=(x-x')^{2}+(y-y')^{2}}$

Подставляя это выражение вместо r , найдём:

${\displaystyle r={\sqrt {\rho ^{2}+z^{2}}}=z{\sqrt {1+{\frac {\rho ^{2}}{z^{2}}}}}}$

Воспользуемся разложением Тейлора в ряд

${\displaystyle {\sqrt {1+u}}=(1+u)^{1/2}=1+{\frac {u}{2}}-{\frac {u^{2}}{8}}+\cdots }$

и выразим r в виде

${\displaystyle r=z{\sqrt {1+{\frac {\rho ^{2}}{z^{2}}}}}=z\left[1+{\frac {\rho ^{2}}{2z^{2}}}-{\frac {1}{8}}\left({\frac {\rho ^{2}}{z^{2}}}\right)^{2}+\cdots \right]=z+{\frac {\rho ^{2}}{2z}}-{\frac {\rho ^{4}}{8z^{3}}}+\cdots }$

Если мы рассмотрим все члены разложения, это будет точным выражением . Подставим это выражение в аргумент экспоненциальной функции под интегралом; ключевую роль в приближении Френеля играет пренебрежение третьим членом в разложении, который предполагается малым. Чтобы это было возможным, он должен слабо влиять на показатель степени. Другими словами, он должен быть намного меньше, чем период показателя экспоненты, то есть ${\displaystyle 2\pi }$ :

${\displaystyle k{\frac {\rho ^{4}}{8z^{3}}}\ll 2\pi .}$

Выражая k в терминах длины волны,

${\displaystyle k={2\pi \over \lambda }}$

получим следующее соотношение:

${\displaystyle {\frac {\rho ^{4}}{z^{3}\lambda }}\ll 8}$

Умножая обе стороны на ${\displaystyle z/\lambda }$ , получим

${\displaystyle {\frac {\rho ^{4}}{z^{2}\lambda ^{2}}}\ll 8{z \over \lambda }}$

или, подставляя ранее полученное выражение для ρ ² ,

${\displaystyle {\frac {[(x-x')^{2}+(y-y')^{2}]^{2}}{z^{2}\lambda ^{2}}}\ll 8{z \over \lambda }}$

Если это условие выполняется для всех значений x , x' , y и y' , тогда мы можем пренебречь третьим членом в разложении Тейлора. Более того, если третий член мал, то все последующие слагаемые более высоких порядков тоже малы, и ими можно пренебречь. Тогда можно аппроксимировать выражение, используя два члена разложения:

${\displaystyle r\approx z+{\frac {(x-x')^{2}+(y-y')^{2}}{2z}}}$

Это выражение называется приближением Френеля , а неравенство, полученное ранее, есть условие применимости этого приближения.

Дифракция Френеля

Условие применимости достаточно слабо и позволяет все характерные размеры взять как сравнимые величины, если апертура много меньше, чем длина пути. К тому же, так как нас интересует только малая область недалеко от источника, величины x и y много меньше, чем z , предположим ${\displaystyle \theta \approx 0}$ , что означает ${\displaystyle \cos \theta \approx 1}$ , и r в знаменателе можно аппроксимировать выражением ${\displaystyle r\approx z}$ .

В противоположность дифракции Фраунгофера , дифракция Френеля должна учитывать кривизну волнового фронта , чтобы правильно учесть относительные интерферирующих волн.

Электрическое поле для дифракции Френеля в точке (x,y,z) дано в виде:

${\displaystyle E(x,y,z)=-{i \over \lambda }{e^{ikz} \over z}\iint _{-\infty }^{+\infty }E(x',y',0)e^{{ik \over 2z}[(x-x')^{2}+(y-y')^{2}]}dx'dy'}$

Это - интеграл дифракции Френеля; он означает, что, если приближение Френеля действительно, распространяющееся поле - волна, начинающаяся в апертуре и движущаяся вдоль z . Интеграл модулирует амплитуду и фазу сферической волны. Аналитическое решение этого выражения возможно только в редких случаях. Для дальнейшего упрощения, действительного только для намного больших расстояний от источника дифракции, см. дифракция Фраунгофера .

См. также

• Дифракция Фраунгофера
• Интегралы Френеля

Примечания

Литература

• Ландау Л. Д. , Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М. : Наука , 1988. — 512 с. — (« Теоретическая физика », том II). — ISBN 5-02-014420-7 .
• Сивухин Д. В. Общий курс физики. — М. . — Т. IV. Оптика.

Ссылки