Рафаэль Бомбелли ( итал. Rafael Bombelli ; ок. 1526, Болонья — 1572, вероятно, Рим ) — итальянский математик , инженер-гидротехник . Настоящая фамилия: Маццоли ( Mazzoli ), ему пришлось сменить фамилию при возвращении в Болонью, потому что его дед был некогда казнён как заговорщик .

Известен тем, что ввёл в математику комплексные числа как легальный объект и разработал базовые правила действий с ними. Перевёл и опубликовал «Арифметику» Диофанта ; благодаря этому событию начинается история теории чисел в Европе.

Биография

Рафаэль Маццоли родился в Болонье в семье торговца шерстью Антонио Маццоли и дочери портного Диаманте Скудьери ( Diamante Scudieri ), он был старшим из шести их детей. Учился архитектуре. Как раз в это время открытия болонского математика дель Ферро в изложении Тартальи вызвали подъём массового интереса к математике, который захватил и Бомбелли .

Будучи по делам в Риме, Бомбелли познакомился с профессором университета Антонио Мария Пацци, который незадолго до того обнаружил в Ватиканской библиотеке рукопись «Арифметики» Диофанта . Друзья договорились перевести её на латинский. Одновременно с переводом Бомбелли пишет свой трактат «Алгебра» в трёх книгах, куда включил не только свои разработки, но и множество задач Диофанта с собственными комментариями. Однако главную ценность труда Бомбелли составили его собственные открытия. Он планировал дополнить трактат ещё двумя книгами геометрического содержания, но не успел их завершить. В 1923 году незаконченные рукописи последних томов «Алгебры» были обнаружены историком и опубликованы в 1929 году.

Научная деятельность

Алгебра

Главный труд Бомбелли — «Алгебра» ( L’Algebra ), написана около 1560 года, издана в 1572 году в Венеции и переиздана в 1579 году в Болонье.

«Алгебра» примечательна во многих отношениях. Бомбелли, первый в Европе, свободно оперирует с отрицательными числами , приводит правила работы с ними, включая правило знаков для умножения. Он также первым, опередив своё время, оценил пользу комплексных чисел , в частности для решения уравнений третьей степени по формулам Кардано .

Пример . Уравнение ${\displaystyle x^{3}=15x+4}$ имеет вещественный корень x = 4 , однако по формулам Кардано получаем: ${\displaystyle x={\sqrt[{3}]{2+11i}}+{\sqrt[{3}]{2-11i}}}$ .

Бомбелли обнаружил, что ${\displaystyle {\sqrt[{3}]{2\pm 11i}}=2\pm i}$ , откуда сразу получается нужный вещественный корень. Он подчеркнул, что в подобных ( неприводимых ) случаях комплексные слагаемые в формуле Кардано всегда сопряжены , поэтому при их сложении получается вещественный корень. Данное уравнение имеет ещё два вещественных корня ( ${\displaystyle -2\pm {\sqrt {3}}}$ ), однако отрицательные значения в тот период ещё не рассматривались как допустимые. Разъяснения Бомбелли положили начало успешному применению в математике комплексных чисел.

Исчерпывающее исследование неприводимого случая требовало умения извлекать корни из комплексных чисел, а этого умения у Бомбелли ещё не было. Полностью проблему решили Виет и де Муавр .

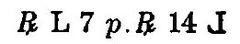
Бомбелли также придумал первые скобки ; они имели вид прямой и зеркально-отражённой буквы L. Привычные нам круглые скобки появились в том же XVI веке, однако в общее употребление их ввели только Лейбниц и Эйлер . Бомбелли первый стал использовать числовое (а не словесное, как ранее) обозначение для показателя степени , помечаемое специальной дужкой снизу. Современное обозначение показателя ввёл в широкое обращение Декарт .

Цепные дроби

Из других научных достижений Бомбелли следует отметить фактическое применение цепных дробей для вычисления квадратных корней из натуральных чисел. Понятия цепной дроби у Бомбелли ещё не было, и ниже излагается алгоритм в более поздней версии, данной Катальди (1613 год) .

Чтобы найти значение ${\displaystyle {\sqrt {n}}}$ , сначала определим его целое приближение: ${\displaystyle {\sqrt {n}}=a\pm r}$ , где ${\displaystyle 0<r<1\ }$ . Тогда ${\displaystyle n=(a\pm r)^{2}=a^{2}\pm 2ar+r^{2}\ }$ . Отсюда несложно вывести, что ${\displaystyle r={\frac {|n-a^{2}|}{2a\pm r}}}$ . Повторно подставляя полученное выражение в формулу ${\displaystyle {\sqrt {n}}=a\pm r}$ , мы получаем разложение в цепную дробь:

${\displaystyle a\pm {\frac {|n-a^{2}|}{2a\pm {\frac {|n-a^{2}|}{2a\pm {\frac {|n-a^{2}|}{2a\pm \cdots }}}}}}}$

Для оценки точности полученных приближений можно использовать одно из свойств цепных дробей: последовательные значения подходящих дробей колеблются около точного значения, чередуя приближения с избытком и недостатком.

Пример. Для ${\displaystyle {\sqrt {13}},a=3}$ мы получаем последовательные приближения:

${\displaystyle 3{\frac {2}{3}},\ 3{\frac {3}{5}},\ 3{\frac {20}{33}},\ 3{\frac {66}{109}},\ 3{\frac {109}{180}},\ 3{\frac {720}{1189}},\ \cdots }$

Последняя дробь равна ${\displaystyle 3.605550883}$ …, в то время как ${\displaystyle {\sqrt {13}}\ \approx 3.605551275}$ .

Другие достижения

Бомбелли занимался древними задачами удвоения куба и трисекции угла и сумел доказать, что их можно свести к решению кубического уравнения .

Память

В честь Бомбелли названы:

• лунный кратер Бомбелли ;
• астероид .

Примечания

Труды

• (итал.).

Литература

• Боголюбов А. Н. Бомбелли Раффаэле // . — Киев: Наукова думка, 1983. — 639 с.
• История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича , в трёх томах. — М. : Наука, 1970. — Т. I.
• Каучикас А. П. Неопределённые уравнения в «Алгебре» Р. Бомбелли // История и методология естественных наук. — Изд. МГУ, 1978. — Т. 20. Математика и механика . — С. 138—146 .
• Смирнова Г. С. Геометрическое решение кубических уравнений в "Алгебре" Рафаэля Бомбелли // История и методология естественных наук. — Изд. МГУ, 1989. — Т. 36. Математика и механика . — С. 123—129 .

Ссылки

• Джон Дж. О’Коннор и Эдмунд Ф. Робертсон . (англ.) — биография в архиве MacTutor .