Interested Article - Интеграл Якоби

- 2020-01-08
- 1
В небесной механике интеграл Якоби является единственной известной сохраняющейся величиной в рамках ограниченной круговой задачи трёх тел. В отличие от задачи двух тел , энергия и момент системы не сохраняются по отдельности и общее аналитическое решение получить не удается. Интеграл Якоби используется для получения численного решения в отдельных случаях.
Определение
Синодическая система
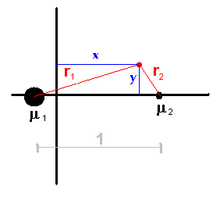
Одной из удобных систем координат является так называемая синодическая система с началом координат в барицентре , при этом линия, соединяющая массы μ 1 и μ 2 , выбрана в качестве оси x , а расстояние между ними выбрано в качестве единицы расстояния. Поскольку система вращается вместе с телами, то они остаются неподвижными и расположенными в точках с координатами (− μ 2 , 0) и (+ μ 1 , 0) 1 .
В системе координат ( x , y ) постоянная Якоби имеет вид
где:
- — ( орбитальный период T),
- , для двух масс m 1 , m 2 и гравитационной постоянной G ,
- — расстояния от тестовой частицы до двух массивных тел.
Заметим, что интеграл Якоби равен минус удвоенной полной энергии в расчёте на единицу массы во вращающейся системе отсчёта: первое слагаемое относится к центробежной потенциальной энергии, второе относится к гравитационному потенциалу, третье — кинетическая энергия. В данной системе отсчёта силы, действующие на частицу, включают две гравитационные силы со стороны тел, центробежную силу и силу Кориолиса . Поскольку первые три силы можно выразить через потенциалы, а последняя перпендикулярна траектории, все они консервативны, поэтому энергия, измеряемая в данной системе энергия (следовательно, и интеграл Якоби), сохраняется.
Сидерическая система

В инерциальной (сидерической) системе отсчёта ( ξ , η , ζ ) массы вращаются вокруг барицентра. В данной системе координат постоянная Якоби имеет вид
Вывод
В синодической системе ускорения можно представить в виде производных от скалярной функции
Рассмотрим уравнения Лагранжа для движения тела:
После умножения уравнений на и соответственно и сложения всех трёх выражений получим равенство
После интегрирования получим выражение
где C J — постоянная интегрирования.
Левая часть равенства является квадратом скорости v пробной частицы в синодической системе отсчёта.
1 Данная система координат является неинерциальной, что объясняет появление слагаемых, связанных с центробежной силой и силой Кориолиса.
Примечания
- от 2 февраля 2017 на Wayback Machine . Jacobi, Carl G. J. Sur le movement d'un point et sur un cas particulier du problème des trois corps (фр.) // : magazine. — 1836. — Vol. 3 . — P. 59—61 .
Литература
- Carl D. Murray and Stanley F. Dermot Solar System Dynamics [Cambridge, England: Cambridge University Press, 1999], pages 68–71. ( ISBN 0-521-57597-4 )
- 2020-01-08
- 1






















