Центрированное квадратное число — это центрированное полигональное число , которое представляет квадрат с точкой в центре и все остальные окружающие точки, находящиеся на квадратных слоях.

Таким образом, каждое центрированное квадратное число равно числу точек внутри данного расстояния в кварталах от центральной точки на квадратной решётке . Центрированные квадратные числа, как и фигурные числа , имеют мало практических приложений, если вообще имеют, но они изучаются в занимательной математике за элегантные геометрические и арифметические свойства.

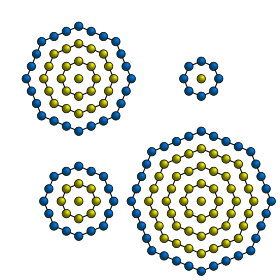
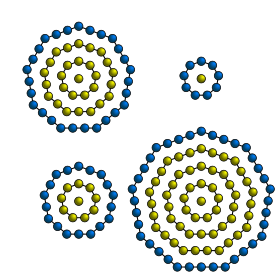
Фигуры для первых четырех центрированных квадратных чисел показаны ниже:

${\displaystyle C_{4,1}=1}$		${\displaystyle C_{4,2}=5}$		${\displaystyle C_{4,3}=13}$		${\displaystyle C_{4,4}=25}$

Связь с другими фигурными числами

n -ое центрированное квадратное число задается формулой

${\displaystyle C_{4,n}=n^{2}+(n-1)^{2}.}$

Другими словами, центрированное квадратное число — это сумма двух последовательных квадратов . Следующие диаграммы демонстрируют формулу:

${\displaystyle C_{4,1}=1}$		${\displaystyle C_{4,2}=1+4}$		${\displaystyle C_{4,3}=4+9}$		${\displaystyle C_{4,4}=9+16}$

Формулу можно представить следующим образом

${\displaystyle C_{4,n}={(2n-1)^{2}+1 \over 2};}$

таким образом, n -ое центрированное квадратное число равно половине n -го нечетного квадрата + 1/2, что иллюстрируется ниже:

${\displaystyle C_{4,1}=(1+1)/2}$		${\displaystyle C_{4,2}=(9+1)/2}$		${\displaystyle C_{4,3}=(25+1)/2}$		${\displaystyle C_{4,4}=(49+1)/2}$

Как и другие центрированные полигональные числа , центрированные квадратные числа могут быть выражены в треугольных числах :

${\displaystyle C_{4,n}=1+4\,T_{n-1},}$

где

${\displaystyle T_{n}={n(n+1) \over 2}={n^{2}+n \over 2}={n+1 \choose 2}}$

есть n -ое треугольное число. Это легко увидеть, если просто удалить центральную точку и разделить оставшиеся на четыре треугольника, как ниже:

${\displaystyle C_{4,1}=1}$		${\displaystyle C_{4,2}=1+4\times 1}$		${\displaystyle C_{4,3}=1+4\times 3}$		${\displaystyle C_{4,4}=1+4\times 6.}$

Разность между двумя последовательными восьмиугольными числами есть центрированное квадратное число (Conway and Guy, p. 50).

Свойства

Первые несколько центрированных квадратных чисел :

1 , 5 , 13 , 25 , 41 , 61 , 85 , 113 , 145 , 181, 221, 265, , 365 , 421, 481, 545, 613, 685, 761, 841, 925, 1013, 1105, 1201, 1301, 1405, 1513, 1625, 1741, 1861, 1985, 2113, 2245, 2381, 2521, 2665, 2813, 2965, 3121, 3281, 3445, 3613, 3785, 3961, 4141, 4325, …

Все центрированные квадратные числа нечетны, и последняя цифра в десятичном представлении дает последовательность 1-5-3-5-1.

Все центрированные квадратные числа и их делители дают остаток 1 при делении на 4. Отсюда все центрированные квадратные числа и их делители сравнимы с 1 или 5 по модулю 6, 8 или 12.

Все центрированные квадратные числа за исключением 1 есть гипотенуза в одном из пифагоровой тройке (например, 3-4-5, 5-12-13).

Центрированные квадратные простые

Центрированные квадратные простые — это центрированные квадратные числа, являющиеся также простыми . В отличие от обычных квадратных чисел , которые никогда не являются простыми, несколько центрированных квадратных чисел просты.

Несколько первых центрированных квадратных простых :

5, 13, 41, 61, 113, 181, 313, 421, 613, 761, 1013, 1201, 1301, 1741, 1861, 2113, 2381, 2521, 3121, 3613, …

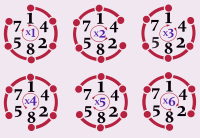
Замечательный пример можно увидеть в магическом квадрате 10-го столетия ал-Антаакии.

См. также

• Число клеток в окрестности фон Неймана порядка r совпадает с центрированным квадратным числом с номером r
• Теорема о представлении простых чисел в виде суммы двух квадратов

Примечания

Литература

• Alfred, U. (1962), " n and n + 1 consecutive integers with equal sums of squares", Mathematics Magazine , 35 (3): 155—164, JSTOR , MR {{ citation }} : templatestyles stripmarker в |title= на позиции 1 ( справка )
• Beiler, A. H. (1964), Recreations in the Theory of Numbers , New York: Dover, p. 125
• Conway, John H. ; Guy, Richard K. (1996), The Book of Numbers , New York: Copernicus, pp. 41—42, ISBN 0-387-97993-X , MR

Ссылки