Interested Article - Центрированное шестиугольное число

- 2020-05-13
- 1
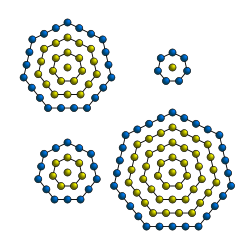
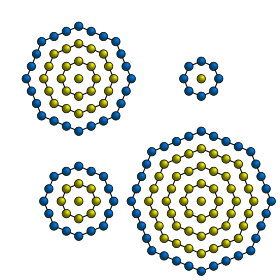
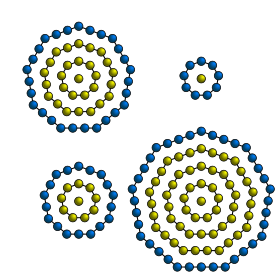
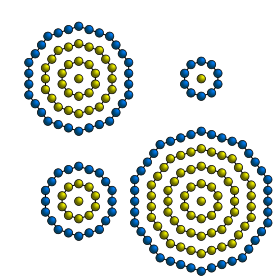
Центрированные шестиугольные числа – это центрированные фигурные числа , которые представляют шестиугольник с точкой в центре и все остальные окружающие точки находятся в шестиугольной решётке .
| 1 | 7 | 19 | 37 | |||
|---|---|---|---|---|---|---|
| +1 | +6 | +12 | +18 | |||
|
|
|
|
|
n -ое центрированное шестиугольное число задается формулой

Представление формулы в виде
показывает, что центрированное шестиугольное число для n на 1 больше чем шестикратная величина ( n −1)-го треугольного числа .
Несколько первых центрированных шестиугольных чисел :
Можно заметить, что по основанию 10 последний знак центрированных шестиугольных чисел имеют последовательность 1-7-9-7-1.
Центрированные шестиугольные числа имеют практическое значение управлении логистики, например , в круглых предметов в больший круглый контейнер, таких как в круглые банки, или упаковке проводов в кабель .
Сумма первых n центрированных шестиугольных чисел равна n 3 . Таким образом, последовательности центрированных шестиугольных пирамидальных чисел и кубических чисел идентичны, но представляют различные (геометрические) формы. С другой стороны, центрированные шестиугольные числа – это разность двух соседних кубов, так что центрированные шестиугольные числа — это фигурное представление кубов. Также, простые центрированные шестиугольные числа есть кубические простые числа .
Разность (2 n ) 2 и n -го центрированного шестиугольного числа равна 3 n 2 + 3 n − 1, а разность (2 n − 1) 2 и n -го центрированного шестиугольного числа есть прямоугольное число .
См. также
Примечания
- Последовательность в OEIS
Ссылки
- Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
- 2020-05-13
- 1