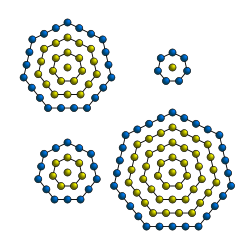
Центрированное десятиугольное число — центрированное фигурное число , которое представляет количество точек в десятиугольнике с точкой в середине и окружающими точками, лежащими на десятиугольных слоях. Центрированное десятиугольное число для n задается формулой

${\displaystyle 5(n^{2}-n)+1}$

Первые несколько центрированных десятиугольных чисел

1 , 11 , 31 , 61 , 101 , 151 , 211, 281, 361, 451, 551, 661, 781, , 1051, … (последовательность в OEIS )

Подобно другим k -угольным числам, n -ое центрированное десятиугольное число можно вычислить, умножая ( n − 1)-ое треугольное число на k , в нашем случае 10, затем добавляя 1. Как следствие, центрированные десятиугольные числа могут быть получены просто добавлением 1 к десятичному представлению числа. Таким образом, все центрированные десятиугольные числа нечётны и всегда кончаются на 1 в десятичном представлении.

Другой результат этой связи с треугольными числами — это простая рекуррентная формула для центрированных десятиугольных чисел

${\displaystyle CD_{n}=CD_{n-1}+10(n-1)}$ ,

где CD ₁ равно 1.

Центрированные десятиугольные простые

Центрированные десятиугольные простые — это центрированное десятиугольное число, которое является простым .

Несколько первых центрированных десятиугольных простых

11, 31, 61, 101, 151, 211, 281, 661, 911, 1051, 1201, 1361, 1531, 1901, 2311, 2531, 3001, 3251, 3511, 4651, 5281, …. (последовательность в OEIS )

Ссылки

• // StateMaster Encyclopedia