Interested Article - Колоссально избыточное число
- 2021-09-06
- 1


Колоссально избыточное число ( CA от англ. colossally abundant number ) — натуральное число , которое в определённом строгом смысле имеет много делителей : существует такое, что для всех :
- ,
где — функция суммы делителей . Все колоссально избыточные числа также являются суперизбыточными числами , но обратное неверно.
Первые 15 колоссально избыточных чисел — 2 , 6 , 12 , 60 , 120 , , , 5040 , 55440, 720720, 1441440 , 4324320, 21621600, 367567200, 6983776800 — также являются первыми 15 весьма суперсоставными числами .
История

Впервые колоссально избыточные числа были изучены Рамануджаном , и его результаты должны были быть включены в его статью 1915 года о сверхсоставном числе . К сожалению, издатель журнала, в который Рамануджан представил свою работу, Лондонское математическое общество , в то время испытывало финансовые затруднения, и Рамануджан согласился удалить некоторые аспекты работы, чтобы снизить стоимость печати . Его выводы в основном были обусловлены гипотезой Римана , и с этим предположением он нашёл верхнюю и нижнюю границы размера колоссально избыточных чисел и доказал, что то, что впоследствии станет известным как неравенство Робина (см. ниже), выполняется для всех достаточно больших значений n .
Класс чисел был пересмотрен в несколько более сильной форме в статье Леонидаса Алаоглу и Пала Эрдёша 1944 года, в которой они пытались расширить результаты Рамануджана .
Свойства
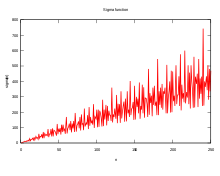
Колоссально избыточные числа — это один из нескольких классов целых чисел, которые пытаются уловить понятие наличия множества делителей. Для положительного целого числа n функция суммы делителей σ ( n ) даёт сумму всех тех чисел, которые делят n , включая 1 и само n . Пауль Бахман показал, что в среднем σ( n ) составляет около π 2 n / 6 . Теорема , тем временем, говорит, что максимальный порядок σ( n ) немного больше, в частности, существует возрастающая последовательность целых чисел n , такая, что для этих целых чисел σ( n ) примерно того же размера, что и e γ n log(log( n )), где γ является постоянной Эйлера — Маскерони . Следовательно, колоссально избыточные числа охватывают понятие наличия множества делителей, требуя от них максимизировать для некоторого , значение функции
по всем значениям . Результаты Бахмана и Грёнвалла гарантируют, что для любого эта функция имеет максимум и что по мере стремления ε к нулю эти максимумы будут увеличиваться. Таким образом, существует бесконечно много колоссально избыточных чисел, хотя они довольно редки, и только 22 из них меньше 10 18 .
Для каждого ε указанная выше функция имеет максимум, но не очевидно, и на самом деле неверно, что для каждого ε это максимальное значение единственно. Алаоглу и Эрдёш изучали, сколько различных значений n может дать одно и то же максимальное значение указанной выше функции для данного значения ε. Они показали, что для большинства значений ε будет единственное целое число n , максимизирующее функцию. Позже, однако, Эрдёш и Жан-Луи Николя показали, что для определённого набора дискретных значений ε может быть два или четыре различных значения n , дающих одно и то же максимальное значение .
В своей статье 1944 года Алаоглу и Эрдёш предположили, что соотношение двух последовательных колоссально избыточных чисел всегда было простым числом . Они показали, что это следует из частного случая в теории трансцендентных чисел , в частности, что для любых двух различных простых чисел p и q только действительные числа t , для которых и p t и q t являются рациональными числами , являются положительными целыми числами. Используя соответствующий результат для трёх простых чисел — частный случай , который К. Л. Зигель доказал, — им удалось показать, что частное двух последовательных колоссально избыточных чисел всегда равно либо простому, либо полупростому числу , то есть числу, состоящему всего из двух простых множителей . Частное никогда не может быть квадратом простого числа.
Гипотеза Алаоглу и Эрдёша остаётся открытой, хотя она проверена как минимум вплоть до 10 7 Если это правда, это будет означать, что существует последовательность неотличимых простых чисел p 1 , p 2 , p 3 ,... таких, что n -е колоссально избыточное число имело вид:
Предполагая, что гипотеза верна, эта последовательность простых чисел начинается с 2, 3, 2, 5, 2, 3, 7, 2 (последовательность в OEIS ). Гипотеза Алаоглу и Эрдёша также означала бы, что никакое значение ε не даёт четырёх различных целых чисел n в качестве максимумов указанной выше функции.
Связь с гипотезой Римана
В 1980-х годах показал , что гипотеза Римана эквивалентна утверждению, что следующее неравенство верно для всех > 5040: (где является постоянной Эйлера — Маскерони ):
Известно, что это неравенство не выполняется для 27 чисел (последовательность в OEIS ):
- 2, 3, 4, 5, 6, 8, 9, 10, 12, 16, 18, 20, 24, 30, 36, 48, 60, 72, 84, 120, 180, 240, 360, 720, 840, 2520, 5040
Робин показал, что если гипотеза Римана верна, то = 5040 — это последнее целое число, для которого она не выполняется. Неравенство теперь известно как неравенство Робина после его работы. Известно, что неравенство Робина, если оно когда-либо не соблюдается, не сработает для колоссально избыточного числа «n»; таким образом, гипотеза Римана фактически эквивалентна неравенству Робина, справедливому для каждого колоссально избыточного числа n > 5040.
В 2001 – 2002 годах Лагариас продемонстрировал альтернативную форму утверждения Робина, которая не требует исключений, используя гармоническое число вместо логарифма :
Или, кроме 8 исключений из n = 1, 2, 3, 4, 6, 12, 24, 60:
Ссылки
- К. Бриггс, Избыточные числа и гипотеза Римана , Экспериментальная математика 15:2 (2006), стр. 251–256, doi : .
- последовательность в OEIS
- С. Рамануджан , " Сверхсоставные числа ", Труды Лондонского математического общества 14 (1915), стр. 347–407, MR : .
- С. Рамануджан, Сборник статей , Челси , 1962.
- С. Рамануджан, "Сверхсоставные числа. Аннотировано с предисловием Ж.-Л. Николя и Г. Робина", Журнал Рамануджана 1 (1997), стр. 119–153.
- Алаоглу, Л. ; Эрдёш, П. (1944), (PDF) , Труды Американского математического общества , 56 : 448—469, doi : , MR . Дата обращения: 15 апреля 2021. Архивировано 12 ноября 2017 года. .
- ↑ Г. Харди , Э. М. Райт, Введение в теорию чисел. 5-е издание , Изд. Оксфордского университета , Оксфорд , 1979.
- ↑ Дж. К. Лагариас, от 10 октября 2014 на Wayback Machine , Американский математический ежемесячник 109 (2002), стр. 534–543.
- П. Эрдёш, Ж.-Л. Николя, "Распределение сверхизбыточных чисел", Бюллетень Французского математического общества 103 (1975), стр. 65–90.
- Н. Дж. А. Слоун , от 16 апреля 2021 на Wayback Machine , Он-лайн энциклопедия целочисленных последовательностей. Фонд OEIS.
- G. Robin, "Большие значения функции суммы делителей и гипотеза Римана", Журнал чистой и прикладной математики 63 (1984), стр. 187–213.
Внешние ссылки
- 2021-09-06
- 1




















