Interested Article - Суперизбыточное число

- 2020-04-12
- 1
Суперизбыточное число ( SA от англ. superabundant ) — натуральное число такое, что для всех выполнено
где — функция делителей (то есть сумма всех положительных делителей числа , включая ).
Первые несколько суперизбыточных чисел : 1 , 2 , 4 , 6 , 12 , 24 , 36 , 48 , 60 , 120 , …. Например, число 5 не является суперизбыточным числом, потому что для 1, 2, 3, 4 и 5 сигма равна 1, 3, 4, 7, 6, и 7/4 > 6/5.
Избыточные числа определялись [ уточнить ] Леонидасом Алаоглу и Палом Эрдёшем . Около 30 страниц статьи Рамануджана 1915 года «Сверхсоставные числа», которые были неизвестны Алаоглу и Эрдёшу, были закрыты [ уточнить ] . Эти страницы были наконец опубликованы в Журнале Рамануджана 1 (1997), 119—153 [ уточнить ] . В разделе 59 этой статьи Рамануджан определяет обобщённые сверхсоставные числа , которые включают в себя суперизбыточные числа.
Свойства
Леонидас Алаоглу и Пал Эрдёш ( 1944 ) доказали, что если суперизбыточно, то существуют и такие, что
где:
- — -е простое число;
То есть, они доказали, что если является суперизбыточным, разложение на простые числа имеет невозрастающие показатели (показатель большего простого числа никогда не больше, чем это меньшее простое число) и что все простые числа вплоть до — множители . Тогда, в частности, любое суперизбыточное число является чётным целым числом, кратным -му простому .
Фактически, последний показатель степени равен 1, кроме случаев, когда равно 4 или 36.
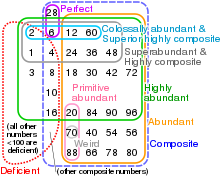
Суперизбыточные числа тесно связаны со сверхсоставными. Не все суперизбыточные числа являются сверхсоставными числами. Фактически, только 449 суперизбыточных и сверхсоставных чисел совпадают (последовательность в OEIS ). Например, 7560 сверхсоставно, но не суперизбыточно. Напротив, 1163962800 суперизбыточно, но не сверхсоставно.
Алаоглу и Эрдёш заметили, что все избыточные числа весьма избыточные .
Не все суперизбыточные числа являются числами харшад . Первым исключением является 105-й номер SA — 149602080797769600. Сумма цифр равна 81, но 81 не делится на этот номер SA равномерно.
Суперизбыточные числа также представляют интерес в связи с гипотезой Римана и в связи с тем, что гипотеза Римана эквивалентна утверждению:
для всех , превышающих наибольшее известное исключение, суперизбыточное число 5040. Если это неравенство имеет больший контрпример, доказывающий ложность гипотезы Римана, наименьший такой контрпример должен быть суперизбыточным числом .
Не все суперизбыточные числа являются колоссально избыточными .
Обобщение
Обобщённые -суперизбыточные числа — такие числа, что для всех , где является суммой -х степеней делителей .
1-суперизбыточные числа — суперизбыточные числа. 0-суперизбыточные числа — сверхсоставные числа.
Например, обобщёнными 2-суперизбыточными числами являются 1, 2, 4, 6, 12, 24, 48, 60, 120, 240, …
Примечания
- последовательность в OEIS
- ↑ Алаоглу, Леонидас ; Эрдёш, Пал (1944), "О cверхсоставных и похожих числах", Труды Американского математического общества , Американское математическое общество , 56 (3): 448—469, doi : , JSTOR [ уточнить ]
- .
- последовательность в OEIS
Литература
- Keith Briggs. Abundant numbers and the Riemann hypothesis // . — 2006. — Т. 15 . — С. 251–256 .
- Amir Akbary, Zachary Friggstad. // American Mathematical Monthly . — 2009. — Т. 116 , вып. 3 . — С. 273–275 . — doi : .
Ссылки
- 2020-04-12
- 1