Сфеническое число ( англ. sphenic number , от др.-греч. σφήν — «клин» ) — натуральное число , равное произведению трёх различных простых чисел (так, например, ${\displaystyle 30=2\cdot 3\cdot 5}$ ; соответственно, число 30 является сфеническим).

Свойства

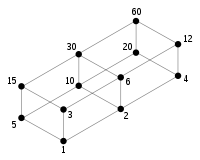
• Количество делителей произвольного сфенического числа всегда равно 8. Например, если ${\displaystyle n=p\cdot q\cdot r}$ , где ${\displaystyle p}$ , ${\displaystyle q}$ и ${\displaystyle r}$ — разные простые числа, то делителями ${\displaystyle n}$ будут ${\displaystyle \left\{1,\ p,\ q,\ r,\ pq,\ pr,\ qr,\ n\right\}}$ . Так первое сфеническое число 30 имеет делители 1, 2, 3, 5, 6, 10, 15 и 30.
  • Обратное, вообще говоря, неверно: например, числа вида ${\displaystyle n=p^{3}\cdot q}$ , где ${\displaystyle p}$ и ${\displaystyle q}$ — разные простые числа, также имеют 8 делителей ${\displaystyle \left\{1,\ p,\ p^{2},\ p^{3},\ q,\ pq,\ p^{2}q,\ n\right\}}$ , но не являются сфеническими.

• Функция Мёбиуса произвольного сфенического числа равна −1 .

Примеры

Сфенические числа образуют последовательность ( в OEIS ):

30 , 42 , 66 , 70 , 78 , 102 , , 110 , , 130 , 138 , 154 , , 170 , , , 186 , , , …

В частности:

• ${\displaystyle 30=2\cdot 3\cdot 5}$
• ${\displaystyle 42=2\cdot 3\cdot 7}$
• ${\displaystyle 66=2\cdot 3\cdot 11}$
• ${\displaystyle 70=2\cdot 5\cdot 7}$
• ${\displaystyle 78=2\cdot 3\cdot 13}$
• ${\displaystyle ...}$

Примером двух последовательных сфенических чисел являются (230 = 2 · 5 · 23) и (231 = 3 · 7 · 11). Примером трёх последовательных сфенических чисел являются (1309 = 7 · 11 · 17), (1310 = 2 · 5 · 131) и (1311 = 3 · 19 · 23). Более чем трёх последовательных сфенических чисел быть не может, поскольку каждое четвёртое натуральное число будет делиться на 4.

Наибольшим известным сфеническим числом является (2 ^82589933 − 1) · (2 ^77232917 − 1) · (2 ^74207281 − 1), произведение трёх крупнейших известных простых чисел (на 07.06.2019) .

См. также

• Полупростое число — число, представимое произведением двух различных простых чисел.

Примечания