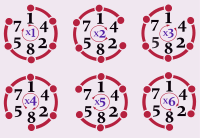
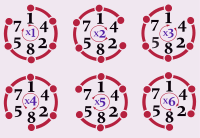
Циклическое число — целое число , циклические перестановки цифр которого являются произведениями этого числа на последовательные числа. Наиболее известный пример такого числа — 142857 :

142857 × 1 = 142857

142857 × 2 = 285714

142857 × 3 = 428571

142857 × 4 = 571428

142857 × 5 = 714285

142857 × 6 = 857142

Детали

Чтобы число было циклическим, требуется, чтобы умножение на последовательные числа давала перестановки цифр числа. Так, число 076923 не считается циклическим, поскольку, хотя все циклические перестановки являются произведением числа на некоторые целые множители , эти множители не являются последовательными целыми числами:

076923 × 1 = 076923

076923 × 3 = 230769

076923 × 4 = 307692

076923 × 9 = 692307

076923 × 10 = 769230

076923 × 12 = 923076

Обычно исключаются следующие типичные случаи:

1. Отдельные цифры, например, 5
2. повторяющиеся цифры, например, 555
3. повторяющиеся циклические числа, такие как 142857142857

Если в числах не разрешены ведущие нули , то 142857 является единственным циклическим числом в десятичной системе счисления , что определяется необходимой структурой чисел, описанной в следующей секции. Если ведущие нули разрешены, последовательность циклических чисел начинается с:

(10 ⁶ −1) / 7 = 142857 (6 цифр)

(10 ¹⁶ −1) / 17 = 0588235294117647 (16 цифр)

(10 ¹⁸ −1) / 19 = 052631578947368421 (18 цифр)

(10 ²² −1) / 23 = 0434782608695652173913 (22 цифры)

(10 ²⁸ −1) / 29 = 0344827586206896551724137931 (28 цифр)

(10 ⁴⁶ −1) / 47 = 0212765957446808510638297872340425531914893617 (46 цифр)

(10 ⁵⁸ −1) / 59 = 0169491525423728813559322033898305084745762711864406779661 (58 цифр)

(10 ⁶⁰ −1) / 61 = 016393442622950819672131147540983606557377049180327868852459 (60 цифр)

(10 ⁹⁶ −1) / 97 = 010309278350515463917525773195876288659793814432989690721649484536082474226804123711340206185567 (96 цифр)

Связь с повторяющимися десятичными числами

Циклические числа связаны с периодическими десятичными дробями долей единицы . Циклическое число длины L имеет десятичное представление

1/( L + 1).

Наоборот, если десятичный период числа 1 / p (где p простое) равен

p − 1,

то цифры представляют циклическое число.

Например:

1/7 = 0.142857 142857….

Умножение этой дроби даёт циклическую перестановку:

1/7 = 0.142857 142857…

2/7 = 0.285714 285714…

3/7 = 0.428571 428571…

4/7 = 0.571428 571428…

5/7 = 0.714285 714285…

6/7 = 0.857142 857142….

Формат циклических чисел

Используя связь с долями единицы, можно показать, что циклические числа имеют вид частного Ферма

${\displaystyle {\frac {b^{p-1}-1}{p}}}$ ,

где b — основание системы счисления (10 для десятичной системы ), а p — простое , которое не делит b . (Простые числа p , которые образуют циклические числа по основанию b , называются или длинными простыми по основанию b ).

Например, для b = 10, p = 7 даёт циклическое число 142857, а для b = 12, p = 5 даёт циклическое число 2497.

Не все значения p дают циклические числа согласно этой формуле. Например, для b = 10, p = 13 даёт 076923076923 ₁₀ , а для b = 12, p = 19 даёт 076B45076B45076B45 ₁₂ . Эти числа не являются циклическими, поскольку состоят из повторяющихся последовательностей.

Первые значения p , для которых формула даёт циклические числа по десятичному основанию ( b = 10) (последовательность в OEIS )

7, 17, 19, 23, 29, 47, 59, 61, 97, 109, 113, 131, 149, 167, 179, 181, 193, 223, 229, 233, 257, 263, 269, 313, 337, 367, 379, 383, 389, 419, 433, 461, 487, 491, 499, 503, 509, 541, 571, 577, 593, 619, 647, 659, 701, 709, 727, 743, 811, 821, 823, 857, 863, 887, 937, 941, 953, 971, 977, 983, …

Для b = 12 ( двенадцатеричная система ) эти значения p равны (последовательность в OEIS )

5, 7, 17, 31, 41, 43, 53, 67, 101, 103, 113, 127, 137, 139, 149, 151, 163, 173, 197, 223, 257, 269, 281, 283, 293, 317, 353, 367, 379, 389, 401, 449, 461, 509, 523, 547, 557, 569, 571, 593, 607, 617, 619, 631, 641, 653, 691, 701, 739, 751, 761, 773, 787, 797, 809, 821, 857, 881, 929, 953, 967, 977, 991, …

Для b = 2 ( двоичная система ) эти значения p равны (последовательность в OEIS )

3, 5, 11, 13, 19, 29, 37, 53, 59, 61, 67, 83, 101, 107, 131, 139, 149, 163, 173, 179, 181, 197, 211, 227, 269, 293, 317, 347, 349, 373, 379, 389, 419, 421, 443, 461, 467, 491, 509, 523, 541, 547, 557, 563, 587, 613, 619, 653, 659, 661, 677, 701, 709, 757, 773, 787, 797, 821, 827, 829, 853, 859, 877, 883, 907, 941, 947, …

Для b = 3 ( троичная система ) эти значения p равны (последовательность в OEIS )

2, 5, 7, 17, 19, 29, 31, 43, 53, 79, 89, 101, 113, 127, 137, 139, 149, 163, 173, 197, 199, 211, 223, 233, 257, 269, 281, 283, 293, 317, 331, 353, 379, 389, 401, 449, 461, 463, 487, 509, 521, 557, 569, 571, 593, 607, 617, 631, 641, 653, 677, 691, 701, 739, 751, 773, 797, 809, 811, 821, 823, 857, 859, 881, 907, 929, 941, 953, 977, …

Не существует таких чисел p в шестнадцатеричной системе .

Известные схемы таких последовательностей получаются из алгебраической теории чисел , а именно, эта последовательность является множество простых p , таких что b является первообразным корнем по модулю p .

Построение циклических чисел

Циклические числа можно получить следующей процедурой :

Пусть b — основание системы счисления (10 для десятичных чисел)
Пусть p — простое число, не являющееся делителем b .
Положим t = 0.
Положим r = 1.
Положим n = 0.
цикл:

Положим t = t + 1

Положим x = r · b

Положим d = целая часть ( x / p )

Положим r = x mod p

Положим n = n · b + d

Если r ≠ 1, переходим в начало цикла.

Если t = p − 1, то n является циклическим числом.

Процедура работает путём вычисления цифр дроби 1 / p по основанию b по алгоритму деления столбиком . На каждом шаге r является остатком , а d является очередной цифрой.

Шаг

n = n · b + d

просто обеспечивает сборку цифр числа. Для компьютеров, не имеющих возможности вычислений с целыми числами очень большого размера, эти цифры можно просто отправлять на печать или собирать другим способом.

Заметим, что при достижении t границы p /2 получившееся число должно быть циклическим и необходимости вычислять дальнейшие цифры нет.

Свойства циклических чисел

Примечание : Ниже нижний индекс означает основание. Так, 142 ₁₀ означает число 142 по основанию 10, а 142 ₅ означает число 142 по основанию 5 (то есть 47 ₁₀ ).

• Если умножить число на генерирующее простое, получим последовательность цифр ́ base −1' (9 в случае десятичного основания). 142857 ₁₀ × 7 = 999999 ₁₀ .
• Если разбить число на группы цифр (по две, три, четыре м т.д. цифры), а затем сложить полученные числа, получим последовательности девяток. 14 + 28 + 57 = 99 , 142 + 857 = 999 , 1428 + 5714+ 2857 = 9999 и т. д. … (Это частный случай теоремы Миди .)
• Все циклические числа делятся на ́ base −1' (9 в случае десятичного основания).

Сколько циклических чисел?

Количество циклических чисел, не превышающих 10 ⁿ , для натуральных n образуют последовательность (последовательность в OEIS ):

1, 9, 60, 467, 3617, 25883, 248881, 2165288, 19016617…

Была высказана гипотеза (пока не доказана), что существует бесконечное множество циклических чисел . Согласно гипотезе Эмиля Артина эта последовательность содержит 37.395..% простых чисел (для b из последовательности A085397; последовательность в OEIS ).

Другие системы счисления

Используя вышеприведённую технику, можно найти циклические числа в других системах счисления.

В двоичной системе последовательность циклических чисел начинается с: (последовательность в OEIS )

11 ₂ =3 ₁₀ → 01 ₂

101 ₂ = 5 ₁₀ → 0011 ₂

1011 ₂ = 11 ₁₀ → 0001011101 ₂

1101 ₂ = 13 ₁₀ → 000100111011 ₂

10011 ₂ =19 ₁₀ → 000011010111100101 ₂

11101 ₂ =29 ₁₀ → 0000100011010011110111001011 ₂

100101 ₂ = 37 ₁₀ → 000001101110101100111110010001010011 ₂

В троичной системе : (последовательность в OEIS )

2 ₃ =2 ₁₀ → 1 ₃

12 ₃ = 5 ₁₀ → 0121 ₃

21 ₃ = 7 ₁₀ → 010212 ₃

122 ₃ = 17 ₁₀ → 0011202122110201 ₃

201 ₃ =19 ₁₀ → 001102100221120122 ₃

1002 ₃ = 29 ₁₀ → 0002210102011122200121202111 ₃

1011 ₃ = 31 ₁₀ → 000212111221020222010111001202 ₃

В четверичной системе:

(циклических чисел нет)

В пятеричной системе: (последовательность в OEIS )

2 ₅ = 2 ₁₀ → 2 ₅

3 ₅ = 3 ₁₀ → 13 ₅

12 ₅ = 7 ₁₀ → 032412 ₅

32 ₅ = 17 ₁₀ → 0121340243231042 ₅

43 ₅ = 23 ₁₀ → 0102041332143424031123 ₅

122 ₅ = 37 ₁₀ → 003142122040113342441302322404331102 ₅

133 ₅ = 43 ₁₀ → 002423141223434043111442021303221010401333 ₅

В шестеричной системе: (последовательность в OEIS )

15 ₆ = 11 ₁₀ → 0313452421 ₆

21 ₆ = 13 ₁₀ → 024340531215 ₆

25 ₆ = 17 ₁₀ → 0204122453514331 ₆

105 ₆ = 41 ₁₀ → 0051335412440330234455042201431152253211 ₆

135 ₆ = 59 ₁₀ → 0033544402235104134324250301455220111533204514212313052541 ₆

141 ₆ = 61 ₁₀ → 003312504044154453014342320220552243051511401102541213235335 ₆

211 ₆ =79 ₁₀ → 002422325434441304033512354102140052450553133230121114251522043201453415503105

В семеричной системе: (последовательность в OEIS )

2 ₇ = 2 ₁₀ → 3 ₇

5 ₇ = 5 ₁₀ → 1254 ₇

14 ₇ = 11 ₁₀ → 0431162355 ₇

16 ₇ = 13 ₁₀ → 035245631421 ₇

23 ₇ = 17 ₁₀ → 0261143464055232 ₇

32 ₇ = 23 ₁₀ → 0206251134364604155323 ₇

56 ₇ = 41 ₁₀ → 0112363262135202250565543034045314644161 ₇

В восьмеричной системе : (последовательность в OEIS )

3 ₈ = 3 ₁₀ → 25 ₈

5 ₈ = 5 ₁₀ → 1463 ₈

13 ₈ = 11 ₁₀ → 0564272135 ₈

35 ₈ = 29 ₁₀ → 0215173454106475626043236713 ₈

65 ₈ = 53 ₁₀ → 0115220717545336140465103476625570602324416373126743 ₈

73 ₈ = 59 ₁₀ → 0105330745756511606404255436276724470320212661713735223415 ₈

123 ₈ = 83 ₁₀ → 0061262710366576352321570224030531344173277165150674112014254562075537472464336045 ₈

В девятеричной системе:

2 ₉ = 2 ₁₀ → 4 ₉

(других нет)

В одиннадцатеричной системе 11: (последовательность в OEIS )

2 ₁₁ = 2 ₁₀ → 5 ₁₁

3 ₁₁ = 3 ₁₀ → 37 ₁₁

12 ₁₁ = 13 ₁₀ → 093425A17685 ₁₁

16 ₁₁ = 17 ₁₀ → 07132651A3978459 ₁₁

21 ₁₁ = 23 ₁₀ → 05296243390A581486771A ₁₁

27 ₁₁ = 29 ₁₀ → 04199534608387A69115764A2723 ₁₁

29 ₁₁ = 31 ₁₀ → 039A32146818574A71078964292536 ₁₁

В двенадцатеричной системе : (последовательность в OEIS )

5 ₁₂ = 5 ₁₀ → 2497 ₁₂

7 ₁₂ = 7 ₁₀ → 186A35 ₁₂

15 ₁₂ = 17 ₁₀ → 08579214B36429A7 ₁₂

27 ₁₂ = 31 ₁₀ → 0478AA093598166B74311B28623A55 ₁₂

35 ₁₂ = 41 ₁₀ → 036190A653277397A9B4B85A2B15689448241207 ₁₂

37 ₁₂ = 43 ₁₀ → 0342295A3AA730A068456B879926181148B1B53765 ₁₂

45 ₁₂ = 53 ₁₀ → 02872B3A23205525A784640AA4B9349081989B6696143757B117 ₁₂

В тринадцатеричной системе: (последовательность в OEIS )

2 ₁₃ = 2 ₁₀ → 6 ₁₃

5 ₁₃ = 5 ₁₀ → 27A5 ₁₃

B ₁₃ = 11 ₁₀ → 12495BA837 ₁₃

16 ₁₃ = 19 ₁₀ → 08B82976AC414A3562 ₁₃

25 ₁₃ = 31 ₁₀ → 055B42692C21347C7718A63A0AB985 ₁₃

2B ₁₃ = 37 ₁₀ → 0474BC3B3215368A25C85810919AB79642A7 ₁₃

32 ₁₃ = 41 ₁₀ → 04177C08322B13645926C8B550C49AA1B96873A6 ₁₃

В 14-ричной системе: (последовательность в OEIS )

3 ₁₄ = 3 ₁₀ → 49 ₁₄

13 ₁₄ = 17 ₁₀ → 0B75A9C4D2683419 ₁₄

15 ₁₄ = 19 ₁₀ → 0A45C7522D398168BB ₁₄

19 ₁₄ = 23 ₁₀ → 0874391B7CAD569A4C2613 ₁₄

21 ₁₄ = 29 ₁₀ → 06A89925B163C0D73544B82C7A1D ₁₄

3B ₁₄ = 53 ₁₀ → 039AB8A075793610B146C21828DA43253D6864A7CD2C971BC5B5 ₁₄

43 ₁₄ = 59 ₁₀ → 03471937B8ACB5659A2BC15D09D74DA96C4A62531287843B21C80D4069 ₁₄

В 15-ричной системе: (последовательность в OEIS )

2 ₁₅ = 2 ₁₀ → 7 ₁₅

D ₁₅ = 13 ₁₀ → 124936DCA5B8 ₁₅

14 ₁₅ = 19 ₁₀ → 0BC9718A3E3257D64B ₁₅

18 ₁₅ = 23 ₁₀ → 09BB1487291E533DA67C5D ₁₅

1E ₁₅ = 29 ₁₀ → 07B5A528BD6ACDE73949C6318421 ₁₅

27 ₁₅ = 37 ₁₀ → 061339AE2C87A8194CE8DBB540C26746D5A2 ₁₅

2B ₁₅ = 41 ₁₀ → 0574B51C68BA922DD80AE97A39D286345CC116E4 ₁₅

В шестнадцатеричной системе :

(циклических чисел нет)

В 17-ричной системе: (последовательность в OEIS )

2 ₁₇ = 2 ₁₀ → 8 ₁₇

3 ₁₇ = 3 ₁₀ → 5B ₁₇

5 ₁₇ = 5 ₁₀ → 36DA ₁₇

7 ₁₇ = 7 ₁₀ → 274E9C ₁₇

B ₁₇ = 11 ₁₀ → 194ADF7C63 ₁₇

16 ₁₇ = 23 ₁₀ → 0C9A5F8ED52G476B1823BE ₁₇

1E ₁₇ = 31 ₁₀ → 09583E469EDC11AG7B8D2CA7234FF6 ₁₇

В 18-ричной системе: (последовательность в OEIS )

5 ₁₈ = 5 ₁₀ → 3AE7 ₁₈

B ₁₈ = 11 ₁₀ → 1B834H69ED ₁₈

1B ₁₈ = 29 ₁₀ → 0B31F95A9GDAE4H6EG28C781463D ₁₈

21 ₁₈ = 37 ₁₀ → 08DB37565F184FA3G0H946EACBC2G9D27E1H ₁₈

27 ₁₈ = 43 ₁₀ → 079B57H2GD721C293DEBCHA86CA0F14AFG5F8E4365 ₁₈

2H ₁₈ = 53 ₁₀ → 0620C41682CG57EAFB3D4788EGHBFH5DGB9F51CA3726E4DA9931 ₁₈

35 ₁₈ =59 ₁₀ → 058F4A6CEBAC3BG30G89DD227GE0AHC92D7B53675E61EH19844FFA13H7 ₁₈

В 19-ричной системе: (последовательность в OEIS )

2 ₁₉ = 2 ₁₀ → 9 ₁₉

7 ₁₉ = 7 ₁₀ → 2DAG58 ₁₉

B ₁₉ = 11 ₁₀ → 1DFA6H538C ₁₉

D ₁₉ = 13 ₁₀ → 18EBD2HA475G ₁₉

14 ₁₉ = 23 ₁₀ → 0FD4291C784I35EG9H6BAE ₁₉

1A ₁₉ = 29 ₁₀ → 0C89FDE7G73HD1I6A9354B2BF15H ₁₉

1I ₁₉ = 37 ₁₀ → 09E73B5C631A52AEGHI94BF7D6CFH8DG8421 ₁₉

В двадцатеричной системе : (последовательность в OEIS )

3 ₂₀ = 3 ₁₀ → 6D ₂₀

D ₂₀ = 13 ₁₀ → 1AF7DGI94C63 ₂₀

H ₂₀ = 17 ₁₀ → 13ABF5HCIG984E27 ₂₀

13 ₂₀ = 23 ₁₀ → 0H7GA8DI546J2C39B61EFD ₂₀

1H ₂₀ = 37 ₁₀ → 0AG469EBHGF2E11C8CJ93FDA58234H5II7B7 ₂₀

23 ₂₀ = 43 ₁₀ → 0960IC1H43E878GEHD9F6JADJ17I2FG5BCB3526A4D ₂₀

27 ₂₀ = 47 ₁₀ → 08A4522B15ACF67D3GBI5J2JB9FEHH8IE974DC6G381E0H ₂₀

В 21-ричной системе: (последовательность в OEIS )

2 ₂₁ = 2 ₁₀ → A ₂₁

J ₂₁ = 19 ₁₀ → 1248HE7F9JIGC36D5B ₂₁

12 ₂₁ = 23 ₁₀ → 0J3DECG92FAK1H7684BI5A ₂₁

18 ₂₁ = 29 ₁₀ → 0F475198EA2IH7K5GDFJBC6AI23D ₂₁

1A ₂₁ = 31 ₁₀ → 0E4FC4179A382EIK6G58GJDBAHCI62 ₂₁

2B ₂₁ = 53 ₁₀ → 086F9AEDI4FHH927J8F13K47B1KCE5BA672G533BID1C5JH0GD9J ₂₁

38 ₂₁ = 71 ₁₀ → 06493BB50C8I721A13HFE42K27EA785J4F7KEGBH99FK8C2DIJAJH356GI0ID6ADCF1G5D ₂₁

В 22-ричной системе: (последовательность в OEIS )

5 ₂₂ = 5 ₁₀ → 48HD ₂₂

H ₂₂ = 17 ₁₀ → 16A7GI2CKFBE53J9 ₂₂

J ₂₂ = 19 ₁₀ → 13A95H826KIBCG4DJF ₂₂

19 ₂₂ = 31 ₁₀ → 0FDAE45EJJ3C194L68B7HG722I9KCH ₂₂

1F ₂₂ = 37 ₁₀ → 0D1H57G143CAFA2872L8K4GE5KHI9B6BJDEJ ₂₂

1J ₂₂ = 41 ₁₀ → 0BHFC7B5JIH3GDKK8CJ6LA469EAG234I5811D92F ₂₂

23 ₂₂ = 47 ₁₀ → 0A6C3G897L18JEB5361J44ELBF9I5DCE0KD27AGIFK2HH7 ₂₂

В 23-ричной системе: (последовательность в OEIS )

2 ₂₃ = 2 ₁₀ → B ₂₃

3 ₂₃ =3 ₁₀ → 7F ₂₃

5 ₂₃ = 5 ₁₀ → 4DI9 ₂₃

H ₂₃ = 17 ₁₀ → 182G59AILEK6HDC4 ₂₃

21 ₂₃ = 47 ₁₀ → 0B5K1AHE496JD4KCGEFF3L0MBH2LC58IDG39I2A6877J1M ₂₃

2D ₂₃ = 59 ₁₀ → 08M51CJK65AC1LJ27I79846E9H3BFME0HLA32GHCAL13KF4FDEIG8D5JB7 ₂₃

3K ₂₃ = 89 ₁₀ → 05LG6ADG0BK9CL4910HJ2J8I21CF5FHD4327B8C3864EMH16GC96MB2DA1IDLM53K3E4KLA7H759IJKFBEAJEGI8 ₂₃

В 24-ричной системе: (последовательность в OEIS )

7 ₂₄ = 7 ₁₀ → 3A6KDH ₂₄

B ₂₄ = 11 ₁₀ → 248HALJF6D ₂₄

D ₂₄ = 13 ₁₀ → 1L795CM3GEIB ₂₄

H ₂₄ = 17 ₁₀ → 19L45FCGME2JI8B7 ₂₄

17 ₂₄ = 31 ₁₀ → 0IDMAK327HJ8C96N5A1D3KLG64FBEH ₂₄

1D ₂₄ = 37 ₁₀ → 0FDEM1735K2E6BG54CN8A91MGKI3L9HC7IJB ₂₄

1H ₂₄ = 41 ₁₀ → 0E14284G98IHDB2M5KBGN9MJLFJ7EF56ACL1I3C7 ₂₄

В 25-ричной системе:

2 ₂₅ = 2 ₁₀ → C ₂₅

(других нет)

Заметим, что для троичного основания ( b = 3) случай p = 2 даёт 1, что по правилам не является циклическим числом (тривиальный случай, одна цифра). Здесь же этот случай приведён для полноты теории, что все числа получаются таким способом.

Можно показать, что циклических чисел (отличных от тривиальных случаев с одной цифрой) не существует в системах счисления с квадратным основанием, то есть с основаниями 4, 9, 16, 25 и т. д..

См. также

• Периодическая дробь
• Малая теорема Ферма

Примечания

Литература

• С.Л. Василенко. (неопр.) .
• Martin Gardner. Mathematical Circus: More Puzzles, Games, Paradoxes and Other Mathematical Entertainments From Scientific American. — New York: The Mathematical Association of America, 1979. — С. 111–122.
  • Мартин Гарднер. Лучшие математические игры и головоломки (Или самый настоящий математический цирк). — Москва: АСТ · Астрель, 2009. — С. 111–121. — ISBN 978-5-17-058244-0 ; 978-5-271-23247-3; УДК 159.9 ББК 88.37.

Литература для дальнейшего чтения

• Dan Kalman. // The College Mathematics Journal. — 1996. — Март ( т. 27 , вып. 2 ). — С. 109–115 .
• John Leslie. . — Longman, Hurst, Rees, Orme, Brown, 1820. — ISBN 1-4020-1546-1 .
• David Wells. The Penguin Dictionary of Curious and Interesting Numbers . — Penguin Press. — ISBN 0-14-008029-5 .

Ссылки

• Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .