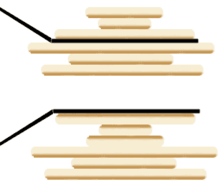
Блинная сортировка (от англ. pancake sorting ) — алгоритм сортировки . Единственная операция, допустимая в алгоритме — переворот элементов последовательности до какого-либо индекса. В отличие от традиционных алгоритмов, в которых минимизируют количество сравнений, в блинной сортировке требуется сделать как можно меньше переворотов. Процесс можно визуально представить как стопку блинов , которую тасуют путём взятия нескольких блинов сверху и их переворачивания.

Алгоритм

Простейший алгоритм (вариант сортировки выбором ) даёт не более ${\displaystyle 2n-3}$ переворотов, однако требует поиска наибольшего элемента . В 1979 году Билл Гейтс и Христос Пападимитриу представили свой алгоритм и доказали достаточность ${\displaystyle (5n+5)/3}$ переворотов и необходимость ${\displaystyle 17n/16}$ . В 1997 году Хейдари и Судборог показали нижнюю границу в ${\displaystyle 15n/14}$ . Они представили точные значения вплоть до ${\displaystyle N=13}$ , для которого требуется 15 переворотов . Значительно (до ${\displaystyle 18n/11}$ ) превзойти результат Гейтса и Пападимитриу получилось только в 2008 году у группы исследователей из Техасского университета в Далласе под руководством Судборога .

Задача о подгоревших блинах

Усложнённый вариант представляет собой блинную сортировку последовательности, элементы которой содержат дополнительный бинарный параметр. Эту задачу предложили Билл Гейтс и Христос Пападимитриу в 1979 году . Она стала известна как «задача о подгоревших блинах» ( англ. burnt pancake problem ):

Каждый блин в стопке подгорел с одной стороны. Требуется отсортировать блины по возрастанию (убыванию) диаметра так, чтобы они все лежали на тарелке подгоревшей стороной вниз.

В 2007 году группа студентов создала биокомпьютер на основе генетически модифицированной кишечной палочки ( E. coli ), который решал задачу о подгорелых блинах. Роль блинов играли фрагменты дезоксирибонуклеиновой кислоты (3′- и 5′-концы которых обозначали разные стороны блина). Бактерия, выстроив фрагменты в нужном порядке, приобретала устойчивость к антибиотику и не погибала. Время, затраченное на поиск правильной комбинации, показывало минимально необходимое число переворотов фрагмента .

Реализация

public static void PancakeSort<T>(IList<T> arr, int cutoffValue = 2)
	where T : IComparable
{
	for (int i = arr.Count - 1; i >= 0; --i)
	{
		int pos = i;
		// Find position of max number between beginning and i
		for (int j = 0; j < i; j++)
		{
			if (arr[j].CompareTo(arr[pos]) > 0)
			{
				pos = j;
			}
		}

		// is it in the correct position already? 
		if (pos == i)
		{
			continue;
		}

		// is it at the beginning of the array? If not flip array section so it is
		if (pos != 0)
		{
			Flip(arr, pos + 1);
		}

		// Flip array section to get max number to correct position    
		Flip(arr, i + 1);
	}
}

private static void Flip<T>(IList<T> arr, int n)
	where T : IComparable
{
	for (int i = 0; i < n; i++)
	{
		--n;
		T tmp = arr[i];
		arr[i] = arr[n];
		arr[n] = tmp;
	}
}

Примечания

См. также

• Ханойская башня

Ссылки

• Weisstein, Eric W. (англ.) . MathWorld. Дата обращения: 16 августа 2009.
• Alexander Bogomolny. (англ.) . Дата обращения: 16 августа 2009. 5 апреля 2012 года.