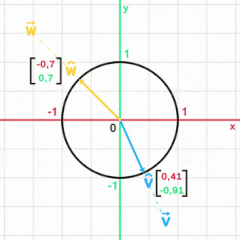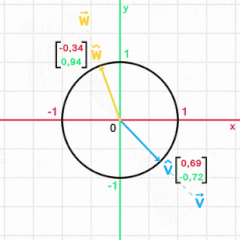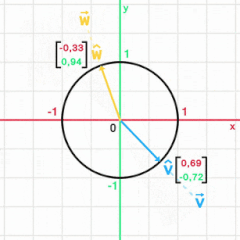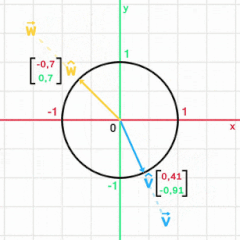
Единичный вектор , или орт , — вектор нормированного пространства , длина которого равна единице. Единичные вектора используются, в частности, для задания направлений в пространстве. Множество единичных векторов образует единичную сферу.

Единичный вектор часто обозначается строчной буквой с крышкой: ${\displaystyle \mathbf {\hat {v}} }$ .

Единичный вектор ${\displaystyle \mathbf {\hat {v}} }$ (нормированный вектор), коллинеарный с заданным ${\displaystyle \mathbf {v} }$ , определяется по формуле

${\displaystyle \mathbf {\hat {v}} ={\frac {\mathbf {\vec {v}} }{\lVert \mathbf {v} \rVert }}=\left({{\frac {\mathbf {\vec {v}} _{x}}{\mathbf {\lVert v\rVert } }},{\frac {\mathbf {\vec {v}} _{y}}{\mathbf {\lVert v\rVert } }},{\frac {\mathbf {\vec {v}} _{z}}{\mathbf {\lVert v\rVert } }}}\right)}$

где ${\displaystyle \mathbf {\lVert {v}\rVert } ={\sqrt {\mathbf {\vec {v}} _{x}+\mathbf {\vec {v}} _{y}+\mathbf {\vec {v}} _{z}}}}$ - есть длина (скаларная величина) вектора ${\displaystyle \mathbf {\vec {v}} }$ .

Стоит также отметить, что компоненты (координаты) единичного вектора ${\displaystyle \mathbf {\hat {v}} }$ являются углами:

• ${\displaystyle \cos \alpha ={\frac {\mathbf {\vec {v}} _{x}}{\mathbf {\lVert v\rVert } }}}$

• ${\displaystyle \cos \beta ={\frac {\mathbf {\vec {v}} _{y}}{\mathbf {\lVert v\rVert } }}}$
• ${\displaystyle \cos \gamma ={\frac {\mathbf {\vec {v}} _{z}}{\mathbf {\lVert v\rVert } }}}$

В качестве базисных часто выбираются именно единичные векторы, так как это упрощает вычисления. Такие базисы называют нормированными .

Другие системы координат

Декартова система координат

Единичные векторы могут представлять собой оси в Декартовой системе координат . К примеру, стандартные единичные векторы в направлениях ${\displaystyle x,y}$ , и ${\displaystyle z}$ в трёхмерном пространстве являются:

${\displaystyle \mathbf {\hat {i}} \,\,\mathbf {=} \,\mathbf {{\begin{bmatrix}1\\0\\0\end{bmatrix}},\,\,} \mathbf {\hat {j}} \,\,\mathbf {=} \,\mathbf {{\begin{bmatrix}0\\1\\0\end{bmatrix}},\,\,} \mathbf {\hat {k}} \,\,\mathbf {=} \,\mathbf {\begin{bmatrix}0\\0\\1\end{bmatrix}} }$

Эти векторы являются взаимно ортогональными и такой базис называют ортонормированным базисом , или стандартным базисом в линейной алгебре .

Для обозночения единичных векторов также используеться и другая нотация, к примеру ${\displaystyle (\mathbf {\hat {x}} ,\mathbf {\hat {y}} ,\mathbf {\hat {z}} )}$ , ${\displaystyle (\mathbf {\hat {x}} _{1},\mathbf {\hat {x}} _{2},\mathbf {\hat {x}} _{3})}$ , ${\displaystyle (\mathbf {\hat {e}} _{x},\mathbf {\hat {e}} _{y},\mathbf {\hat {e}} _{z})}$ , или ${\displaystyle (\mathbf {\hat {e}} _{1},\mathbf {\hat {e}} _{2},\mathbf {\hat {e}} _{3})}$ .

Общие обозначения

Общая нотация единичных векторов встречается в физике и геометрии .

Единичный вектор	Нотация	Диаграмма
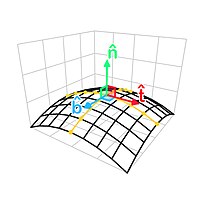
Вектор касательной	${\displaystyle \mathbf {\hat {t}} }$	Образование вектора нормали ${\displaystyle \mathbf {\hat {n}} }$ к плоскости при помощи радиального вектора ${\displaystyle r\mathbf {\hat {r}} }$ , а также углового компонента поворота ${\displaystyle \theta {\boldsymbol {\hat {\theta }}}}$ необходимо для того чтобы векторные уравнения углового движения выполнялись.
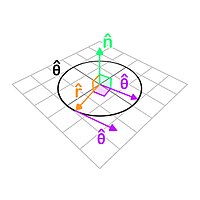
Вектор нормали к поверхности/плоскости содержащей радиальный компонент и угловой компонент	${\displaystyle \mathbf {\hat {n}} =\mathbf {\hat {r}} \times {\boldsymbol {\hat {\theta }}}}$
Бинормальный вектор к касательной и нормали	${\displaystyle \mathbf {\hat {b}} =\mathbf {\hat {t}} \times \mathbf {\hat {n}} }$
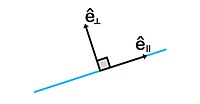
Единичный вектор коллинеарен к оси/линии	${\displaystyle \mathbf {\hat {e}} _{\parallel }}$	Единичный вектор ${\displaystyle \mathbf {\hat {e}} _{\parallel }}$ выровнен параллельно в неком направлении (голубая линия), и ортогональный единичный вектор ${\displaystyle \mathbf {\hat {e}} _{\bot }}$ .
Единичный вектор ортогонален к оси/линии	${\displaystyle \mathbf {\hat {e}} _{\bot }}$
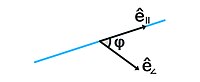
Единичный вектор отклонен на некий угол относительно оси/линии	${\displaystyle \mathbf {\hat {e}} _{\angle }}$	Единичный вектор ${\displaystyle \mathbf {\hat {e}} _{\angle }}$ отклонен на угол φ (от 0 до ${\displaystyle \pi }$ /2 радиан) относительно оси/линии.

См. также

• Единичный отрезок
• Прямоугольная система координат
• Полярная система координат

Примечания

В статье не хватает ссылок на источники (см. рекомендации по поиску ). Информация должна быть проверяема , иначе она может быть удалена. Вы можете статью, добавив ссылки на авторитетные источники в виде сносок . ( 7 июня 2019 )

В другом языковом разделе есть более полная статья (англ.) . Вы можете помочь проекту, расширив текущую статью с помощью перевода