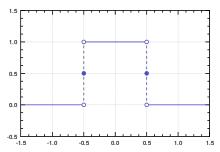
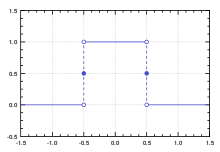
Прямоуго́льная фу́нкция , едини́чный и́мпульс , прямоуго́льный импульс , или нормированное прямоугольное окно́ — кусочно-постоянная функция следующего вида:

${\displaystyle \mathrm {rect} (t)=\sqcap (t)={\begin{cases}0,&|t|>{\frac {1}{2}}\\[3pt]{\frac {1}{2}},&|t|={\frac {1}{2}}\\[3pt]1,&|t|<{\frac {1}{2}}\end{cases}}}$

В этом определении в точках разрыва значение функции определено равным 1/2, но возможно определение этих значений иным способом, например, равным 0 и другими вариантами.

Другое определение функции через функцию Хевисайда ${\displaystyle \theta (t)}$ :

${\displaystyle \mathrm {rect} \left({\frac {t}{\tau }}\right)=\theta \left(t+{\frac {\tau }{2}}\right)-\theta \left(t-{\frac {\tau }{2}}\right),}$

или, иначе:

${\displaystyle \mathrm {rect} (t)=\theta \left(t+{\frac {1}{2}}\right)-\theta \left(t-{\frac {1}{2}}\right).}$

Значение функции в точках разрыва зависит от определения значения функции Хевисайда в её точке разрыва.

Интеграл прямоугольной функции по всей прямой:

${\displaystyle \int \limits _{-\infty }^{\infty }\mathrm {rect} (t)\,dt=1.}$

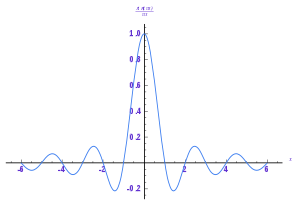
Спектр прямоугольной функции

Спектральный образ прямоугольной функции:

${\displaystyle {\frac {1}{\sqrt {2\pi }}}\int \limits _{-\infty }^{\infty }\mathrm {rect} (t)\cdot e^{-i\omega t}\,dt={\frac {1}{\sqrt {2\pi }}}\cdot \mathrm {sinc} \left({\frac {\omega }{2}}\right),}$

${\displaystyle \mathrm {sinc} \left({\frac {\omega }{2}}\right)={\frac {\mathrm {sin} \left(\omega /2\right)}{\left(\omega /2\right)}}}$ — ненормированная sinc-функция .

При использовании нормированной sinc-функции:

${\displaystyle \int \limits _{-\infty }^{\infty }\mathrm {rect} (t)\cdot e^{-i2\pi ft}\,dt=\mathrm {sinc} (f).}$

Свёртка прямоугольных функций

Треугольная функция может быть определена как свёртка двух прямоугольных функций:

${\displaystyle \mathrm {tri} (t)=\mathrm {rect} (t)*\mathrm {rect} (t)\;.}$

На основе бесконечнократных свёрток прямоугольных функций, длины которых убывают в геометрической прогрессии , строятся атомарные функции .

См. также

• Преобразование Фурье
• Треугольная функция
• Функция Хевисайда
• Атомарная функция

В статье не хватает ссылок на источники (см. рекомендации по поиску ). Информация должна быть проверяема , иначе она может быть удалена. Вы можете статью, добавив ссылки на авторитетные источники в виде сносок . ( 3 марта 2023 )