Ква́дрика , или квадри́ка ,  — n -мерная гиперповерхность в n + 1-мерном пространстве, заданная как множество нулей многочлена второй степени . Если ввести координаты { x ₁ , x ₂ , ..., x _{n +1} } (в евклидовом или аффинном пространстве) , общее уравнение квадрики имеет вид

${\displaystyle \sum _{i,j=1}^{n+1}x_{i}Q_{ij}x_{j}+\sum _{i=1}^{n+1}P_{i}x_{i}+R=0.}$

Это уравнение можно переписать более компактно в матричных обозначениях:

${\displaystyle xQx^{T}+Px^{T}+R=0}$

где x = { x ₁ , x ₂ , ..., x _{n +1} } — вектор -строка, x ^T — транспонированный вектор, Q — матрица размера ( n +1)×( n +1) (предполагается, что хотя бы один её элемент ненулевой), P — вектор-строка, а R — константа. Наиболее часто рассматривают квадрики над действительными или комплексными числами. Определение можно распространить на квадрики в проективном пространстве , см. .

Более общо, множество нулей системы полиномиальных уравнений известно как алгебраическое многообразие . Таким образом, квадрика является ( аффинным или проективным ) алгебраическим многообразием второй степени и коразмерности 1.

Квадрики в евклидовом пространстве

Квадрики на евклидовой плоскости соответствуют случаю n = 1, то есть являются кривыми . Обычно их называют не квадриками, а кониками или коническими сечениями .

Квадрики в (трёхмерном действительном) евклидовом пространстве имеют размерность n = 2 и называются поверхностями второго порядка . Проведя ортогональную замену базиса , любую квадрику в евклидовом пространстве можно привести к нормальной форме. В трёхмерном евклидовом пространстве существует 17 таких форм. Из них 5 являются невырожденными (то есть матрица ${\displaystyle {\begin{pmatrix}Q&{\dfrac {P^{T}}{2}}\\{\dfrac {P}{2}}&R\end{pmatrix}}}$ является невырожденной ). Вырожденные формы включают в себя плоскости, прямые, точки и даже квадрики без действительных точек.

Невырожденные действительные квадрики в евклидовом пространстве
Эллипсоид	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1}$
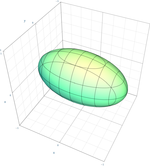
Эллиптический параболоид	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-z=0}$
Гиперболический параболоид	${\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}-z=0}$
Однополостный гиперболоид	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=1}$
Двуполостный гиперболоид	${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=-1}$

Аффинное и проективное пространство

Классификация квадрик в трёхмерном аффинном пространстве совпадает с классификацией квадрик в евклидовом пространстве. Различие состоит в том, что любые две квадрики из одного класса можно перевести друг в друга аффинным преобразованием , тогда как соответствующее ортогональное преобразование существует не всегда (например, эллипсоид ${\displaystyle x^{2}+y^{2}+z^{2}=1}$ невозможно перевести движением в эллипсоид ${\displaystyle 2x^{2}+2y^{2}+2z^{2}=1}$ ).

От квадрики в аффинном пространстве можно перейти к квадрике в проективном пространстве , введя однородные координаты . Пусть в аффинном пространстве введены координаты ${\displaystyle (x_{1},x_{2},\ldots x_{n+1}),}$ тогда в уравнении квадрики достаточно домножить линейные члены на ${\displaystyle x_{0},}$ а свободный член на ${\displaystyle x_{0}^{2}.}$ Уравнение проективной квадрики в однородных координатах имеет вид

${\displaystyle Q(x)=\sum _{ij}a_{ij}x_{i}x_{j}=0.}$

Без ограничения общности можно считать, что матрица ${\displaystyle Q}$ симметрична, то есть ${\displaystyle a_{ij}=a_{ji}.}$ Проективная квадрика называется невырожденной, если соответствующая ей квадратичная форма невырождена .

В действительном проективном пространстве, согласно закону инерции квадратичных форм , любую невырожденную квадратичную форму можно ( проективным преобразованием ) привести к виду

${\displaystyle Q(x)=\pm x_{0}^{2}\pm x_{1}^{2}\pm \cdots \pm x_{n+1}^{2}}$

Поскольку сигнатура квадратичной формы является её инвариантом , в размерности n = 2 существует ровно три класса эквивалентности :

${\displaystyle Q(x)={\begin{cases}x_{0}^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}\\x_{0}^{2}+x_{1}^{2}+x_{2}^{2}-x_{3}^{2}\\x_{0}^{2}+x_{1}^{2}-x_{2}^{2}-x_{3}^{2}\end{cases}}}$

Эллипсоид, эллиптический параболоид и двуполостный гиперболоид принадлежат второму классу, а гиперболический параболоид и однополостный гиперболоид — третьему (последние две квадрики являются примерами линейчатых поверхностей ). Ни одна квадрика в действительном проективном пространстве не принадлежит первому классу, так как соответствующее уравнение определяет пустое множество . В комплексном проективном пространстве все невырожденные квадрики эквивалентны.

Произношение термина

• В словарях приводятся различные ударения: квадри́ка («русское» произношение) и ква́дрика («иностранное» произношение).
• В разговорном языке используется произношение как квадри́ка (Калининградская геометрическая школа), так и ква́дрика . Не известно примеров другого произношения.

Литература

• Математическая энциклопедия . В пяти томах. Том 2, стр.795 (статья «Квадрика»). М.: Советская энциклопедия, 1979—1985.

Примечания

См. также

• Коническое сечение
• Коническая константа
• Кривая второго порядка
• Кубика
• Поверхность второго порядка
• Теорема Брианшона
• Теорема Паскаля
• Фигуры Лиссажу