Коническое сечение
- 1 year ago
- 0
- 0
Важное свойство проективной плоскости — « симметрия » ролей, которые играют точки и прямые в определениях и теоремах, и двойственность является формализацией этой концепции. Имеются два подхода к концепции двойственности: один, использующий язык « », позволяет объявить ряд теорем двойственными друг к другу, при этом двойственная к верной теореме тоже верна; и другой, , основанный на специальном отображении двойственности. Связь между подходами состоит в том, что двойственная теорема получается применением отображения двойственности к каждому объекту исходной. Возможен и .
Концепция двойственности плоскости легко расширяется до двойственности в любой конечномерной проективной геометрии.
Принцип двойственности для проективной плоскости утверждает, что если взять любое верное утверждение, сформулированное в терминах проективной геометрии, (любую проективную теорему), и заменить все вхождения каждого термина на двойственный к нему, получится снова верное утверждение. В частности, для утверждений о точках и прямых достаточно заменить каждое вхождение слова «точка» на «прямая», а «прямая» на «точка» (заменив также окружающие их слова соответствующим образом, например «лежит на» на «принадлежит»). О полученном таким образом утверждении говорят, что оно двойственно исходному. Например, для проективной аксиомы «Через каждые две точки проходит единственная прямая» двойственным утверждением является другая проективная аксиома «Каждые две прямые пересекаются в одной точке».
Этот принцип даёт хороший повод для употребления «симметричного» термина для отношения инцидентности . Так, вместо предложения «точка лежит на прямой» можно сказать «точка и прямая инцидентны», и для превращения утверждения в двойственное достаточно слова точка и прямая переставить местами («прямая и точка инцидентны»).
Эта концепция может быть обобщена до двойственности трёхмерного проективного пространства, где понятия «точки» и «плоскости» меняются ролями (а прямые остаются прямыми). Это приводит к Принципу двойственности для пространства . Возможны и дальнейшие обобщения (см. далее).
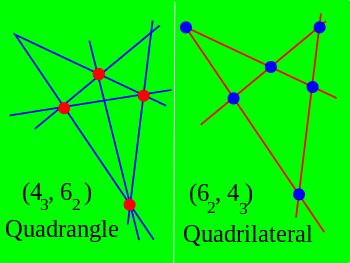
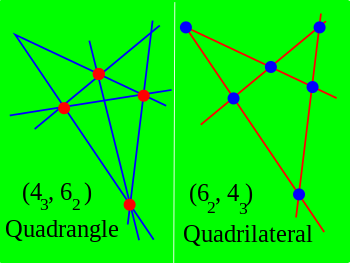
Конфигурацией точек и прямых с символом называют набор из точек и прямых таких, что через каждую точку проходит ровно прямых конфигурации, а на каждой прямой ровно точек конфигурации. Двойственным объектом к конфигурации с символом оказывается конфигурация с символом . Например, к полному четырёхвершиннику двойственным объектом является полный четырёхсторонник .
Принцип двойственности допускает обобщение на произвольные кривые на проективной плоскости. Для построения двойственной кривой строят двойственную (см. ) к каждой точке данной кривой прямую, а потом рассматривают их огибающую — такую кривую, что все полученные прямые являются к ней касательными. В частности, для кривых второго порядка на проективной плоскости оказывается, что двойственная кривая тоже является кривой второго порядка.
Более общо, для квадрик в проективном пространстве имеет место следующее утверждение: множество касательных гиперплоскостей к невырожденной квадрике в проективном пространстве образует невырожденную квадрику в пространстве (звёздочка, как обычно, означает сопряжённое пространство ) . Можно расширить двойственность и на произвольные проективные алгебраические многообразия.
Для вещественной проективной плоскости существует ряд хорошо известных утверждений, двойственных друг другу. Среди них:
В стереометрии имеет место двойственность многогранников , когда точки двойственны граням, а рёбра двойственны рёбрам, так что, например, икосаэдр двойственен додекаэдру , а куб двойственен октаэдру . Одним из способов построения этой двойственности является применение проективной двойственности.
Если определять проективную плоскость аксиоматически как структуру инцидентности в терминах множества точек , множества прямых и бинарного отношения инцидентности , которое определяет, какие точки лежат на каких прямых, то можно определить двойственную структуру плоскости .
Если обменять ролями «точки» и «прямые» в структуре инцидентности
получим двойственную структуру
где — обратное отношение к . является также проективной плоскостью, которая называется дуальной (двойственной) плоскостью для .
Если и изоморфны, то называется самодвойственной . Проективные плоскости для любого поля (или, в более общем случае, для любого тела , изоморфного двойственному себе) являются самодвойственными. В частности, дезарговы плоскости конечного порядка всегда самодвойственны. Однако среди недезарговых плоскостей существуют как самодвойственные (например, ), так и не самодвойственные (например, плоскости Холла).
Двойственность (плоскости) — это отображение из проективной плоскости в её дуальную , сохраняющее свойство инцидентности. Таким образом, двойственность отображает точки в прямые и прямые в точки ( и ) таким образом, что если точка лежит на прямой (обозначается ), то .
Двойственность, определённая таким образом, не обязательно является биекцией. Двойственность проективных плоскостей, являющуюся изоморфизмом, называют корреляцией . Иногда ограничиваются только случаем автоморфизма, то есть отображения из проективной плоскости в себя, тогда существование корреляции означает самодвойственность проективной плоскости.
Можно смотреть на понятие корреляции как на аналог понятия коллинеации. Коллинеация — отображение между проективными плоскостями, отображающее точки в точки, а прямые в прямые, то есть сохраняющее инцидентность.
Важным свойством коллинеаций является то, что они сохраняют двойное отношение . Корреляции тоже удовлетворяют этому требованию, переводя двойное отношение точек в двойное отношение прямых. Таким образом, при переводе множества точек на прямой в пучок прямых через точку каждая гармоническая четвёрка точек переводится в гармоническую четвёрку прямых.
Рассмотрев композицию произвольной корреляции самой с собой, мы автоматически получаем некоторую коллинеацию . Если это оказывается тождественное отображение, то есть если сама корреляция является инволюцией , то она называется поляритетом или полярным соответствием . Иногда это название применяют только к соответствию конкретного вида, см. .
Отображения с теми же свойствами могут быть введены и в пространствах более высоких размерностей, все рассуждения повторяются дословно.
Так как композиция двух корреляций — коллинеация, это позволяет классифицировать коллинеации, после чего множество всех корреляций описывается как композиция фиксированной корреляции со всеми коллинеациями.
Понятие коллинеации тесно связано с понятием проективного преобразования . Формально, проективным преобразованием называют такую коллинеацию, которая происходит из линейного оператора на . Оказывается, в вещественном случае или при эти понятия просто совпадают. Для проективной плоскости вида , где — тело, по любая коллинеация является композицией автоморфизма и проективного преобразования .
При помощи этого можно показать, что корреляция на задаётся произвольной полуторалинейной формой на ассоциированной с произвольным антиавтоморфизмом поля . При этом каждое подпространство отображается в ортогональное ему относительно данной формы.
Двойственность проективной плоскости является частным случаем двойственности для проективных пространств , преобразований (которые обозначаются также ), где — поле, обменивающих объекты размерности с объектами размерности (= коразмерность ). Таким образом, в проективном пространстве размерности точки (размерность 0) будут соответствовать гиперплоскостям (коразмерность 1), прямые, проходящие через две точки (размерность 1), будут соответствовать пересечению двух гиперплоскостей (коразмерность 2), и так далее.
Точки можно рассматривать как ненулевые вектора в ( )-мерном векторном пространстве над , в котором мы отождествляем вектора, отличающиеся умножением на скаляр. Ненулевой вектор в также определяет ортогональное ему -мерное подпространство (гиперплоскость) :
Вектор , используемый для определения гиперплоскости, обозначим , а для обозначения точки, соответствующей концу вектора, будем использовать обозначение . В терминах обычного скалярного произведения , . Поскольку является полем, скалярное произведение симметрично, что означает . Можно задать корреляцию между точками и гиперплоскостями. Это соответствие можно распространить на прямые, образованные двумя точками и пересечение двух гиперплоскостей, и так далее.
На проективной плоскости с полем мы имеем соответствие: однородные координаты прямые, задаваемые уравнениями . В проективном пространстве соответствие выглядит как точки в однородных координатах ↔ плоскости, задаваемые уравнениями . Это соответствие также отображает прямую, задаваемую двумя точками и , в прямую, которая является пересечением двух плоскостей, задаваемых уравнениями и .
Скалярное произведение в можно заменить на произвольную невырожденную билинейную форму, тем самым построив другие корреляции.
Соответствие в в однородных координатах может быть описано геометрически. Для этого используется модель вещественной проективной плоскости «единичная сфера с отождествлением антиподов », или, что эквивалентно, модель прямых и плоскостей, проходящих через начало координат пространства . Сопоставим прямой, проходящей через начало координат, единственную ортогональную ей плоскость, содержащую начало координат. Если в этой модели прямые считать точками, а плоскости — прямыми проективной плоскости , это сопоставление становится соответствием (а фактически — полярным отображением) проективной плоскости. Сферическую модель можно получить как пересечение прямых и плоскостей, проходящих через начало координат, с единичной сферой, имеющей центр в начале координат. Прямые пересекают сферу в двух противоположных точках, которые отождествляются для получения точки проективной плоскости, плоскости же пересекают сферу по большим кругам , которые являются прямыми проективной плоскости.
То, что такое сопоставление «сохраняет» инцидентность, легко показать на модели прямых и плоскостей. Точка, инцидентная прямой в проективной плоскости, соответствует прямой, лежащей на плоскости в модели. При двойственности плоскость становится прямой, проходящей через начало координат и перпендикулярной плоскости. Этот образ (прямая) перпендикулярен любой прямой, лежащей на исходной плоскости, а в частности и исходной прямой (точке проективной плоскости). Все прямые, перпендикулярные исходной прямой, образуют плоскость, которая является образом исходной прямой. Таким образом, образ прямой лежит в образе плоскости, так что инцидентность сохранена.
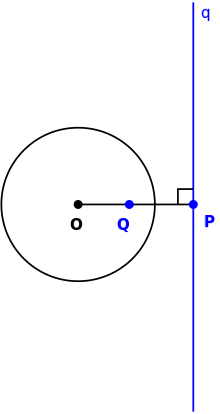
На евклидовой плоскости зафиксируем окружность с центром и радиусом . Для каждой точки , отличной от , определим образ на луче по правилу . Так определенное отображение называется инверсией относительно окружности . Прямая , проходящая через , перпендикулярная , называется полярой точки по отношению к окружности .
Пусть — прямая, не проходящая через . Опустим перпендикуляр из из точки на прямую . Пусть — образ точки при инверсии относительно . Тогда говорят, что — полюс прямой . Если точка лежит на прямой (не проходящей через ), то полюс прямой лежит на поляре точки и наоборот. Таким образом, отображение, при котором точки и прямые переходят в их поляры и полюсы по отношению к , сохраняет инцидентность и является проективным преобразованием .
Чтобы сделать этот процесс взаимно-однозначным преобразованием и превратить в корреляцию , евклидову плоскость необходимо расширить до проективной плоскости путём добавления и , которые лежат на этой бесконечно удалённой прямой. На этой расширенной плоскости мы определяем поляру точки как прямую на бесконечности (а точка является полюсом бесконечно удалённой прямой), и полюсы прямых, проходящих через как точки на бесконечности, где, если прямая имеет угловой коэффициент , её полюс является бесконечно удалённой точкой, соответствующей классу параллельных прямых с наклоном . Полюс для оси — это точка на бесконечности вертикальных прямых, а полюс оси — точка на бесконечности горизонтальных прямых.
Построение полярного преобразования для инверсии относительно окружности, данное выше, можно обобщить с использованием инверсии относительно конических сечений (на расширенной вещественной плоскости). Взаимное преобразование, построенное таким образом, является проективной корреляцией порядка 2, то есть полярным преобразованием.
Модель проективной плоскости с единичной сферой изоморфна (принимая во внимание свойство инцидентности) планарной модели, где плоскость расширена проективной прямой на бесконечности. В этой модели противоположные точки сферы (относительно центра) считаются одной точкой.
Чтобы сопоставить точкам сферы точки на плоскости, положим, что сфера касается плоскости в некоторой точке и эту точку мы выберем в качестве начала координат плоскости. Теперь проведём прямую через точку на сфере и центр сферы. Эта прямая пересечёт сферу в некоторой точке. Полученную точку можно использовать для построения взаимно однозначного отображения
Если точки в заданы в однородных координатах , то
Прямые на планарной модели являются проекциями больших окружностей сферы, поскольку через прямую на плоскости и начало 3-мерных координат можно провести плоскость, и эта плоскость будет пересекать сферу по большой окружности.
Как можно видеть, любой большой окружности на сфере можно сопоставить проективную точку, соответствующую единственной прямой, перпендикулярной плоскости, на которой окружность лежит и которую можно определить как двойственную. Эта прямая пересекает касательную плоскость, и это показывает, каким образом сопоставить единственную точку плоскости любой прямой этой плоскости, таким образом, что точка будет двойственной к прямой.
Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .