Interested Article - Лемма Соллертинского

Ле́мма Соллерти́нского — утверждение проективной геометрии .

Пусть $P$ — произвольная точка и $f$ — проективное преобразование. Тогда множество точек пересечения $l$ и $f(l)$ , где $l$ — прямая, проходящая через $P$ , есть коника , проходящая через точки $P$ и $f(P).$

Доказательство

Пусть $a$ , $b$ , $c$ — прямые, проходящие через точку $P$ , $A$ , $B$ , $C$ — точки пересечения $a$ и $f(a)$ , $b$ и $f(b)$ , $c$ и $f(c)$ . Пять точек $A$ , $B$ , $C$ , $P$ , $f(P)$ , притом единственную. Пусть вторая точка пересечения прямой $d$ , проходящей через $P$ , с этой коникой, $D'$ , а точка пересечения прямой $f(d)$ с этой коникой, $D''$ . Тогда равны следующие двойные отношения : $(A;B;C;D')=(a;b;c;d)=(f(a);f(b);f(c);f(d))=(A,B,C,D'')$ . Значит, $D'=D''$ , то есть прямые $d$ и $f(d)$ переекаются на той же конике. В силу произвольности выбора прямой $d$ на ней лежат все такие точки пересечения, что и требовалось.

История

Лемма названа в честь петербургского математика Н. Соллертинского, использовавшего её при доказательстве в 1896 году . На самом деле это утверждение было известно до Соллертинского; приписывается оно ещё Якобу Штейнеру .

Частные случаи, обобщения и следствия

Если $f$ — движение плоскости, сохраняющее ориентацию фигур, то полученная коника будет окружностью. Это равносильно теореме о вписанном угле .
Если $f$ — движение плоскости, изменяющее ориентацию фигур, то полученная коника будет . Это следует из того, что описанная коника проходит через ортоцентр треугольника тогда и только тогда, когда она является равносторонней гиперболой.
Двойственное к лемме Соллертинского утверждение звучит так:

Пусть $l$ — произвольная прямая и $f$ — проективное преобразование. Тогда все прямые $Pf(P)$ , где $P$ — точка, лежащая на $l$ , касаются коники , касающейся прямых $l$ и $f(l).$

Обратно, всякое гармоническое соответствие двух прямых на плоскости (соответствие между их точками, сохраняющее двойные отношения) получается таким образом: выбирается коника $Q$ , касающаяся обеих прямых $\ell ,\ell '$ , в точке $x\in \ell$ проводится касательная к $Q$ , отличная от $\ell$ , и берется точка ее пересечения с $\ell '$ .
Если $\ell ,\ell '$ — две скрещивающиеся прямые в пространстве, и $f\colon \ell \to \ell '$ — соответствие, сохраняющее двойные отношения, то прямая $xf(x)$ заметает некую квадрику . Они будут составлять одно из двух семейств прямых на ней, а $\ell$ и $\ell '$ будут относиться к другому семейству.

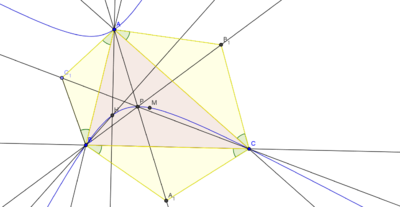
Пусть на сторонах произвольного треугольника $ABC$ построили во внешнюю (внутреннюю) сторону подобные равнобедренные треугольники $ABC'$ , $ACB'$ , $BCA'$ . Тогда прямые $AA'$ , $BB'$ , $CC'$ пересекаются в одной точке, лежащей на описанной гиперболе, проходящей через центроид и ортоцентр — гиперболе Киперта .
Если два треугольника , причём центры ортологии совпадают, то они перспективны.
- Это утверждение Соллертинский использовал при доказательстве теоремы Сонда.
- Из него также следует, что если два треугольника полярны , то они перспективны.

Примечания

Акопян А. В. , Заславский А. А. . Геометрические свойства кривых второго порядка. — 2-е изд., дополн.. — М. : МЦНМО , 2011. — 148 с. — ISBN 978-5-94057-732-4 .