Трапецоэдр ( дельтоэдр , антитегум ) — двойственный антипризме многогранник . Если у исходной антипризмы основания — n-угольники, то у соответствующего ей трапецоэдра есть 2n граней, имеющих форму дельтоида .

Называются трапецоэдры по количеству углов у основания антипризмы, двойственными к которой они являются. Например, четырёхугольный трапецоэдр — это многогранник, двойственный четырёхугольной антипризме.

Треугольный трапецоэдр (если его грани правильные четырёхугольники, то он является кубом)	Четырёхугольный трапецоэдр
Пятиугольный трапецоэдр	Шестиугольный трапецоэдр

Варианты симметрии 4 n 2 плосконосых мозаик: 3.3.n.3.n
Симметрия	Сферияеские		Евклидовы	Компактные гиперболические				Паракомпактные
	222	322	442	552	662	772	882	∞∞2
Тела с отсечёнными вершинами
Конфиг.			3.3.4.3.4
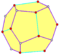
Повёрнытые тела
Конфиг.	V3.3.2.3.2	V3.3.3.3.3	V3.3.4.3.4	V3.3.5.3.5	V3.3.6.3.6	V3.3.7.3.7	V3.3.8.3.8	V3.3.∞.3.∞

Семейство V. n .3.3.3
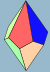
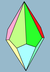
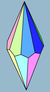
Многогранники
Мозаики
Конфиг.	V2.3.3.3		V4.3.3.3	V5.3.3.3				...	...	...

Примечания