Interested Article - Эннеракт
- 2021-06-28
- 1
| Эннеракт | |
|---|---|
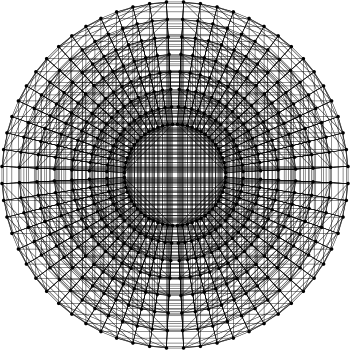
|
|
| Тип | Правильный девятимерный политоп |
| Символ Шлефли | {4,3,3,3,3,3,3,3} |
| 8-мерных ячеек | 18 |
| 7-мерных ячеек | 144 |
| 6-мерных ячеек | 672 |
| 5-мерных ячеек | 2016 |
| 4-мерных ячеек | 4032 |
| Ячеек | 5376 |
| Граней | 4608 |
| Рёбер | 2304 |
| Вершин | 512 |
| Вершинная фигура | Правильный 8-симплекс |
| Двойственный политоп | |
Эннеракт , или 9-гиперкуб , или октадекаиоттон — это девятимерный гиперкуб , аналог куба в девятимерном пространстве . Определяется как выпуклая оболочка 512 точек .
Связанные политопы
Двойственное эннеракту тело - , девятимерный аналог октаэдра .
Если применить к эннеракту альтернацию (удаление чередующихся вершин), можно получить однородный девятимерный многогранник, называемый , который является представителем семейства полугиперкубов .
Свойства
Если у эннеракта — длина ребра , то существуют следующие формулы для вычисления основных характеристик тела:
9-
гиперобъём
:
8-
гиперобъём
гиперповерхности:
Радиус описанной гиперсферы:
Радиус вписанной гиперсферы:
Состав
Эннеракт состоит из:
- 18 октерактов
- 144 гептеракта
- 672 гексеракта
- 2016 пентерактов
- 4032 тессеракта
- 5376 кубов или ячеек
- 4608 квадратов или граней
- 2304 отрезка или ребра
- 512 точек или вершин
Визуализация
Эннеракт можно визуализировать либо параллельным, либо центральным проецированием. В первом случае обычно применяется косоугольная параллельная проекция, которая представляет собой 2 равных гиперкуба размерности n-1, один из которых может быть получен в результате параллельного переноса второго (для эннеракта это 2 октеракта ), вершины которых попарно соединены. Во втором случае обычно используют диаграмму Шлегеля , которая выглядит как гиперкуб размерности n-1, вложенный в гиперкуб той же размерности, у которых вершины также попарно соединены (для эннеракта проекция представляет собой октеракт , вложенный в другой октеракт).
Также применяются и другие способы проецирования.
Ссылки
- Коксестер, Правильные политопы , (третье издание, 1973), Dover edition, ISBN 0-486-61480-8
| Основные выпуклые правильные и однородные политопы в размерностях 2—10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A n | B n | I₂(p) / D n | E₆ / / E₈ / F₄ / G₂ | |||||||||
| Правильный многоугольник | Правильный треугольник | Квадрат |
Правильный
p-угольник |
Правильный шестиугольник | Правильный пятиугольник | |||||||
| Однородный многогранник | Правильный тетраэдр | Правильный октаэдр • Куб | Полукуб | Правильный додекаэдр • Правильный икосаэдр | ||||||||
| Пятиячейник | 16-ячейник • Тессеракт | Полутессеракт | 24-ячейник | 120-ячейник • 600-ячейник | ||||||||
| Правильный 5-симплекс | 5-ортоплекс • 5-гиперкуб | 5-полугиперкуб | ||||||||||
| Правильный 6-симплекс | 6-ортоплекс • 6-гиперкуб | • | ||||||||||
| Правильный 7-симплекс | • 7-гиперкуб | • • | ||||||||||
| Правильный 8-симплекс | • 8-гиперкуб | • • | ||||||||||
| Правильный 9-симплекс | • 9-гиперкуб | |||||||||||
| Правильный 10-симплекс | • 10-гиперкуб | |||||||||||
| Однородный n - политоп | Правильный n - симплекс | n - ортоплекс • n - гиперкуб | n - полугиперкуб | • • | n - пятиугольный многогранник | |||||||
| Темы: Семейства политопов • Правильные политопы • Список правильных политопов и их соединений | ||||||||||||
- 2021-06-28
- 1
![{\displaystyle [\pm 1,\pm 1,\pm 1,\pm 1,\pm 1,\pm 1,\pm 1,\pm 1,\pm 1]}](/images/005/640/5640891/2.jpg?rand=169688)