Interested Article - Ромбододекаэдр

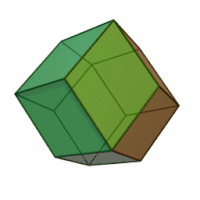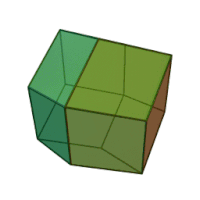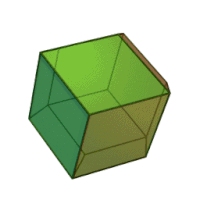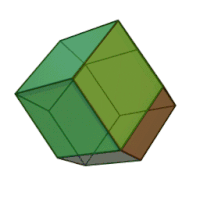
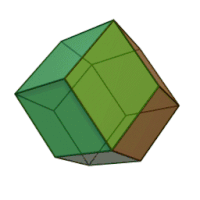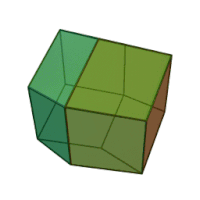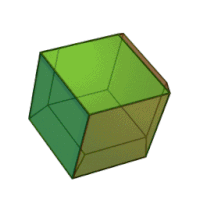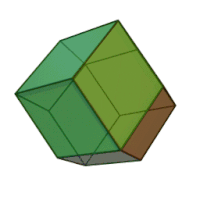
Ромбододекаэдр

Тип	Полуправильный многогранник (каталаново тело)
Грань	Ромб (с острым углом ~70,53 градуса)
Граней	12
Рёбер	24
Вершин	14
Граней при вершинах	4 при 6 вершинах, 3 при 8 вершинах
Группа симметрии	Октаэдрическая ( O _h )
Двойственный многогранник	Кубооктаэдр

Ромбододека́эдр (от « ромб », др.-греч. δώδεκᾰ «двенадцать» и ἕδρα «сиденье») — двенадцатигранник , составленный из одинаковых ромбов . У ромбододекаэдра 14 вершин , 6 из которых являются вершинами меньших углов 4 ромбов, а 8 — вершинами 3 ромбов при их больших углах. Острый угол каждого ромба ${\textstyle \arccos {\frac {1}{3}}\approx 70^{\circ }31'44''}$ , а тупой ${\textstyle 180^{\circ }-\arccos {\frac {1}{3}}\approx 109^{\circ }28'16''}$ . Другими словами: отношение большей диагонали ромба к меньшей равно ${\textstyle {\sqrt {2}}}$ . Одинаковыми ромбододекаэдрами можно заполнить трёхмерное пространство без промежутков и наложений. Взаимное расположение плоскостей граней ромбододекаэдра называется ромбическим (при октаэдрической симметрии) (и также называется положение самих граней). Такое же положение имеют, например, 12 из 18 квадратных граней ромбокубооктаэдра .

Ромбододекаэдр можно собрать из двух равных кубов , разрезав один из них на 6 одинаковых пирамид , квадратные основания которых — 6 граней куба, а вершины совпадают с его центром, и затем приложив эти пирамиды к 6 граням другого куба. А куб можно собрать из 4 ромбододекаэдров, разрезав 3 из них на 4 равные части каждый по противоположным вершинам и четвертям плоскости. Противоположные вершины фрагментов являются вершинами куба, а расстояния между ними — рёбрами куба. Сегменты выстраивают квадратную грань сложением сечений в одной плоскости. Ещё ромбододекаэдр можно собрать из октаэдра и 2 тетраэдров, разрезав тетраэдры на 4 равные части каждый по вершинам. Основание правильной треугольной пирамиды (сегмента тетраэдра) соединяется с гранью октаэдра.

Построение и особенности:

Правильный ромбододекаэдр можно составить из 12 одинаковых ромбов, у которых отношение диагоналей ромбов идентично отношению диагонали квадрата к его стороне. Построение диагоналей ромбов производится циркулем и линейкой без разметки (при случайной длине стороны). Отмечается первая диагональ ромба. Методом построения равнобедренного треугольника циркулем находится перпендикуляр. По заданной пропорции на перпендикуляре отмечается вторая диагональ, значения подгоняются под размеры ромба, диагонали пересекаются в своих серединах. Вершины правильного ромбододекаэдра совпадают с пересечением куба и октаэдра, а диагонали ромбов — с его рёбрами. У правильного ромбододекаэдра 14 вершин — при 8 из них сходятся меньшие диагонали ромбов, а при 6 из них — большие.

Интересный факт: правильными ромбододекаэдрами одинакового объёма можно замостить пространство без промежутков и наложений. У этого замощения две группы стыковки — по 4 и по 6 ромбододекаэдров при одной вершине. Меньшие диагонали в стыковке образуют кубические соты, а большие — тетраэдрально-октаэдрические. Тетраэдрально-октаэдрические соты состоят из правильных тетраэдров и октаэдров — четырёхугольных бипирамид.

Также у ромбододекаэдра 8 вершин содержат сегменты тетраэдра, а остальные 6 — сегменты куба. Здесь под сегментом понимается пирамида, основание которой является гранью тела, а вершина — центром тела. Если ромбододекаэдр по 8 вершинам дополнить оставшимися сегментами до тетраэдров, получится звёздчатый октаэдр. Но если дополнить по 6 вершинам оставшимися сегментами до кубов, получится пространственный крест.

Ромбододекаэдр можно разбить на 4 равных параллелепипеда, у которых все грани равны граням ромбододекаэдра.

Вокруг одного ромбододекаэдра может вместиться 26 ромбододекаэдров одинакового объёма, причём в однослойном заполнении по глубине относительно исходного многогранника