Четырёхска́тный ку́пол — один из многогранников Джонсона ( J ₄ = (по Залгаллеру ) М ₅ ). Его можно получить как срез ромбокубооктаэдра . Как и у всех куполов , многоугольник в основании имеет удвоенное число рёбер и вершин по сравнению с верхним многоугольником. В нашем случае основанием является восьмиугольник .

Многогранник Джонсона — один из 92 строго выпуклых многогранников , имеющих правильные грани, но не являющийся однородным (то есть он не правильный , не архимедов , не призма или антипризма ). Название многограннику дал Норман Джонсон , который первым перечислил эти многогранники в 1966 году .

Формулы

Следующие формулы для объёма , площади поверхности и радиуса описанной сферы могут быть использованы, если все грани являются правильными многоугольниками со сторонами a :

${\displaystyle V=(1+{\frac {2{\sqrt {2}}}{3}})a^{3}\approx 1.94281...a^{3}}$

${\displaystyle A=(7+2{\sqrt {2}}+{\sqrt {3}})a^{2}\approx 11.5605...a^{2}}$

${\displaystyle C=({\frac {1}{2}}{\sqrt {5+2{\sqrt {2}}}})a\approx 1.39897...a}$

Связанные многогранники и соты

Другие выпуклые куполы

Семейство выпуклых куполов

n	2	3	4	5	6
Название	{2} || t{2}	{3} || t{3}	{4} || t{4}	{5} || t{5}	{6} || t{6}
Купол	Диагональный купол	Трёхскатный купол		Пятискатный купол	Шестискатный купол (плоский)
Связанные однородные многогранники	Треугольная призма	Кубооктаэдр	Ромбокубо- октаэдр	Ромбоикосо- додекаэдр

Двойственный многогранник

Двойственный многогранник для четырёхскатного купола имеет 8 треугольных и 4 дельтоидных граней:

Двойственный многогранник для четырёхскатного купола	Развёртка двойственного многогранника

Скрещенный квадратный купол

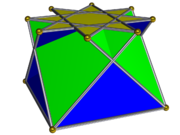
— один из невыпуклых изоморфов многогранника Джонсона , который топологически идентичен выпуклому четырёхскатному куполу. Он может быть получен как срез или квазиромбокубооктаэдра, что аналогично получению купола как среза ромбокубооктаэдра. Как и у всех куполов , многоугольник в основании имеет удвоенное число рёбер и вершин по сравнению с верхним многоугольником. В нашем случае основанием является октаграмма .

Соты

Четырёхскатный купол является компонентой некоторых неоднородных заполняющих пространство рёшёток:

• с тетраэдрами ;
• с кубами и кубооктаэдрами
• с тетраэдрами, квадратными пирамидами и различными комбинациями кубов, удлинённых четырёхугольных пирамид и удлинённых четырёхугольных бипирамид .

Примечания

Ссылки

• , (англ.) Вайсстайн, Эрик , MathWorld