Interested Article - Пятиугольная бипирамида

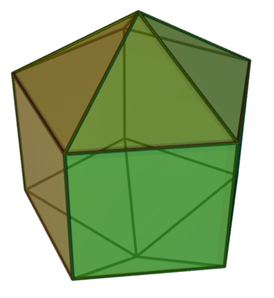
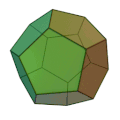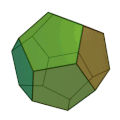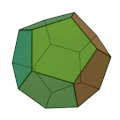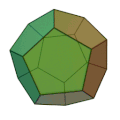
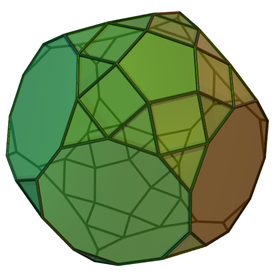
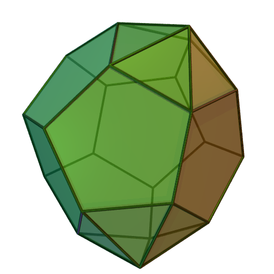
Пятиугольная бипирамида (или дипирамида ) — третье тело в бесконечном семействе изоэдральных бипирамид. Каждая бипирамида является двойственным многогранником для однородных призм .

Хотя тело является изоэдральным , оно не является правильным , поскольку в некоторых вершинах сходятся четыре грани , в других — пять граней.

Свойства

Если грани являются правильными треугольниками , тело является дельтаэдром и многогранником Джонсона ( J ₁₃ , по Залгаллеру — 2M ₃ ). Тело можно рассматривать как две пятиугольные пирамиды ( J ₂ = M ₃ ), соединённые по базисам.

Многогранник Джонсона — это один из 92 строго выпуклых многогранников , имеющих правильные грани, но не являющихся однородными (то есть, они не являются правильными многогранниками , архимедовыми телами , призмами или антипризмами ). Многогранники названы именем Нормана Джонсона , описавшего эти многогранники в 1966 году .

Пятиугольная бипирамида является 4-связной , что означает, что нужно удалить четыре вершины, чтобы оставшиеся вершины не были связны. Тело является одним из четырёх 4-связных симплициальных хорошо покрытых многогранников, что означает, что все максимальные независимые множества его вершин имеют один и тот же размер. Другие три многогранника с таким свойством — это правильный октаэдр , плосконосый двуклиноид и неправильный многогранник с 12 вершинами и 20 треугольными гранями .

Связанные многогранники

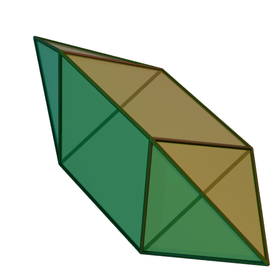
Пятиугольная бипирамида , dt{2,5}, принадлежит последовательности усечений — полное усечение , rdt{2,5}, усечение , trdt{2,5} и ( отсечение вершин ), srdt{2,5}:

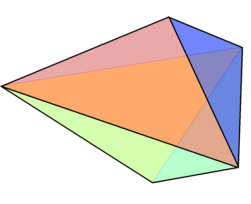
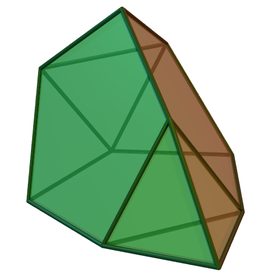
Двойственный многогранник пятиугольной пирамиды с правильными гранями (тела Джонсона) — это пятиугольная призма с 7 гранями — 5 прямоугольных граней и 2 пятиугольника.

Двойственная пятиугольная бипирамида	Развёртка двойственного тела

См. также

Семейство бипирамид
Конфигурация		V3.4.4	V4.4.4							...
Многогранник
Мозаика

Примечания

, с. 169—200.
, с. 894–912.

Литература

Arthur S. Finbow, Bert L. Hartnell, Richard J. Nowakowski, Michael D. Plummer. On well-covered triangulations. III // Discrete Applied Mathematics. — 2010. — Т. 158 , вып. 8 . — С. 894–912 . — doi : .
Norman W. Johnson. // . — 1966. — Т. 18 . — С. 169–200 . — doi : .