Удлинённый пятискатный купол
- 1 year ago
- 0
- 0
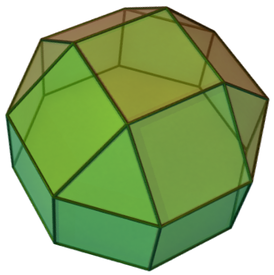
Удлинённый четырёхска́тный ку́пол — один из многогранников Джонсона ( J 19 , по Залгаллеру — М 5 +П 8 ).
Составлен из 18 граней: 4 правильных треугольников , 13 квадратов и 1 правильного восьмиугольника . Восьмиугольная грань окружена восемью квадратными; среди квадратных граней 4 окружены восьмиугольной и тремя квадратными, 4 — восьмиугольной, двумя квадратными и треугольной, 1 — четырьмя квадратными, остальные 4 — двумя квадратными и двумя треугольными; каждая треугольная грань окружена тремя квадратными.
Имеет 36 рёбер одинаковой длины. 8 рёбер располагаются между восьмиугольной и квадратной гранями, 16 рёбер — между двумя квадратными, остальные 12 — между квадратной и треугольной.
У удлинённого четырёхскатного купола 20 вершин. В 8 вершинах сходятся восьмиугольная и две квадратных грани; в остальных 12 — три квадратных и треугольная.
Удлинённый четырёхскатный купол можно получить из двух многогранников — четырёхскатного купола ( J 4 ) и правильной восьмиугольной призмы , все рёбра у которой равны, — приложив их друг к другу восьмиугольными гранями.
Кроме того, удлинённый четырёхскатный купол можно получить из ромбокубооктаэдра , отсекши от того один четырёхскатный купол. Вершины полученного многогранника — 20 из 24 вершин ромбокубооктаэдра, рёбра — 36 из 48 рёбер ромбокубооктаэдра; отсюда ясно, что у удлинённого четырёхскатного купола тоже существуют описанная и полувписанная сферы , причём они совпадают с описанной и полувписанной сферами исходного ромбокубооктаэдра.
Если удлинённый четырёхскатный купол имеет ребро длины , его площадь поверхности и объём выражаются как
Радиус описанной сферы (проходящей через все вершины многогранника) при этом будет равен
радиус полувписанной сферы (касающейся всех рёбер в их серединах) —
Удлинённый четырёхскатный купол с длиной ребра можно расположить в декартовой системе координат так, чтобы его вершины имели координаты
При этом ось симметрии многогранника будет совпадать с осью Oz, а две из четырёх плоскостей симметрии — с плоскостями xOz и yOz.
С помощью удлинённых четырёхскатных куполов можно замостить трёхмерное пространство без промежутков и наложений вместе с правильными тетраэдрами и кубами ; вместе с кубами и кубооктаэдрами ; вместе с удлинёнными четырёхугольными пирамидами ( J 8 ) и удлинёнными четырёхугольными бипирамидами ( J 15 ) — последние два многогранника можно также разрезать на кубы и квадратные пирамиды ( J 1 ) ( ).