Четырёхскатный прямой бикупол
- 1 year ago
- 0
- 0
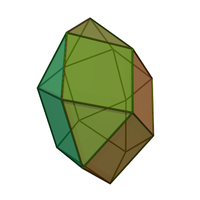
Четырёхскатный повёрнутый бикупол — один из многогранников Джонсона ( J 29 = (по Залгаллеру ) М 5 + М 5 ). Подобно четырёхскатному прямому бикуполу ( J 28 = 2М 5 ), он может быть получен соединением двух четырёхскатных куполов ( J 4 = М 5 ) по их основаниям. Разница лишь в том, что в этом многограннике половинки повёрнуты относительно друг друга на 45º.
Многогранник Джонсона — это один из 92 строго выпуклых многогранников , имеющих правильные грани, но не являющийся однородным (то есть, он не правильный , не архимедов , не призма или антипризма ). Название многограннику дал , который первым перечислил эти многогранники в 1966 .
Четырёхскатный повёрнутый бикупол является вторым в бесконечном множестве повёрнутых бикуполов .
С квадратным повёрнутым бикуполом связан удлинённый четырёхскатный повёрнутый бикупол . Этот многогранник получается, если вставить восьмиугольную призму между двумя половинками четырёхскатного повёрнутого бикупола. Есть споры, является ли удлинённый четырёхскатный повёрнутый бикупол архимедовым телом , поскольку, хотя многогранник удовлетворяет всем остальным требованиям, многогранник не вполне симметричен.
Следующие формулы для объёма и площади поверхности могут быть использованы, если все грани являются правильными со стороной a :
Четырёхскатный повёрнутый бикупол
образует заполняющие пространство соты с
тетраэдрами
, кубами и
кубооктаэдрами
.
Четырёхскатный повёрнутый бикупол
образует заполняющие пространство соты с
тетраэдрами
,
квадратными пирамидами
и комбинацией из кубов,
удлинённых четырёхугольных пирамид
и
удлинённых четырёхугольных бипирамид
)
.