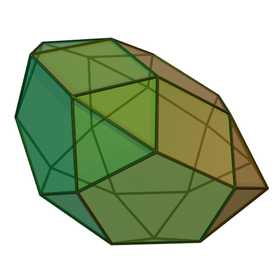
Пятиска́тная повёрнутая куполорото́нда — один из многогранников Джонсона ( J ₃₃ , по Залгаллеру — М ₆ + М ₉ ).

Составлена из 27 граней: 15 правильных треугольников , 5 квадратов и 7 правильных пятиугольников . Среди пятиугольных граней 1 окружена пятью квадратными, 5 — квадратной и четырьмя треугольными, 1 — пятью треугольными; каждая квадратная грань окружена двумя пятиугольными и двумя треугольными; среди треугольных граней 5 окружены тремя пятиугольными, 5 — двумя пятиугольными и треугольной, 5 — двумя квадратными и треугольной.

Имеет 50 рёбер одинаковой длины. 10 рёбер располагаются между пятиугольной и квадратной гранями, 25 рёбер — между пятиугольной и треугольной, 10 рёбер — между квадратной и треугольной, остальные 5 — между двумя треугольными.

У пятискатной повёрнутой куполоротонды 25 вершин. В 10 вершинах сходятся две пятиугольных и две треугольных грани; в 5 вершинах — пятиугольная, две квадратных и треугольная; в остальных 10 — пятиугольная, квадратная и две треугольных.

Пятискатную повёрнутую куполоротонду можно получить из двух других многогранников Джонсона — пятискатного купола ( J ₅ ) и пятискатной ротонды ( J ₆ ), — приложив их друг к другу десятиугольными гранями так, чтобы параллельные десятиугольным пятиугольные грани двух многогранников оказались повёрнуты относительно друг друга на 36°.

Метрические характеристики

Если пятискатная повёрнутая куполоротонда имеет ребро длины ${\displaystyle a}$ , её площадь поверхности и объём выражаются как

${\displaystyle S={\frac {1}{4}}\left(20+15{\sqrt {3}}+7{\sqrt {25+10{\sqrt {5}}}}\right)a^{2}\approx 23{,}5385323a^{2},}$

${\displaystyle V={\frac {5}{12}}\left(11+5{\sqrt {5}}\right)a^{3}\approx 9{,}2418083a^{3}.}$

Примечания

Ссылки

• Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .