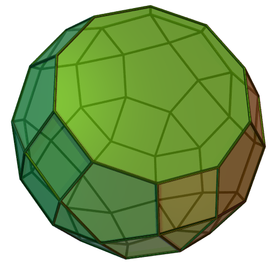
Ко́со скру́ченный отсечённый ромбоикосододека́эдр — один из многогранников Джонсона ( J ₇₈ , по Залгаллеру — М ₁₃ +М ₆ + М ₆ ).

Составлен из 52 граней: 15 правильных треугольников , 25 квадратов , 11 правильных пятиугольников и 1 правильного десятиугольника . Десятиугольная грань окружена пятью пятиугольными и пятью квадратными; среди пятиугольных граней 3 окружены десятиугольной и четырьмя квадратными, 2 — десятиугольной, тремя квадратными и треугольной, 3 — пятью квадратными, остальные 3 — четырьмя квадратными и треугольной; среди квадратных граней 1 окружена десятиугольной, двумя пятиугольными и квадратной, 4 — десятиугольной, двумя пятиугольными и треугольной, 4 — двумя пятиугольными, квадратной и треугольной, 11 — двумя пятиугольными и двумя треугольными, остальные 5 — пятиугольной, квадратной и двумя треугольными; среди треугольных граней 5 окружены пятиугольной и двумя квадратными, остальные 10 — тремя квадратными.

Имеет 105 рёбер одинаковой длины. 5 рёбер располагаются между десятиугольной и пятиугольной гранями, 5 рёбер — между десятиугольной и квадратной, 45 рёбер — между пятиугольной и квадратной, 5 рёбер — между пятиугольной и треугольной, 5 рёбер — между двумя квадратными, остальные 40 — между квадратной и треугольной.

У косо скрученного отсечённого ромбоикосододекаэдра 55 вершин. В 10 вершинах сходятся десятиугольная, пятиугольная и квадратная грани; в 45 вершинах сходятся пятиугольная, две квадратных и треугольная грани.

Косо скрученный отсечённый ромбоикосододекаэдр можно получить из ромбоикосододекаэдра , выбрав в нём две части — любые два не противолежащих и не пересекающихся пятискатных купола ( J ₅ ), — и один из них удалив, а другой повернув на 36° вокруг его оси симметрии. Описанная и полувписанная сферы полученного многогранника совпадают с описанной и полувписанной сферами исходного ромбоикосододекаэдра.

Косо скрученный отсечённый ромбоикосододекаэдр — один из четырёх наименее симметричных многогранников Джонсона (наряду с J ₇₉ , J ₈₂ и J ₈₇ ): его группа симметрии C _s состоит из тождественного преобразования и одной зеркальной симметрии .

Метрические характеристики

Если косо скрученный отсечённый ромбоикосододекаэдр имеет ребро длины ${\displaystyle a}$ , его площадь поверхности и объём выражаются как

${\displaystyle S={\frac {1}{4}}\left(100+15{\sqrt {3}}+\left(10+11{\sqrt {5}}\right){\sqrt {5+2{\sqrt {5}}}}\right)a^{2}\approx 58{,}1146508a^{2},}$

${\displaystyle V={\frac {1}{6}}\left(115+54{\sqrt {5}}\right)a^{3}\approx 39{,}2912785a^{3}.}$

Радиус описанной сферы (проходящей через все вершины многогранника) при этом будет равен

${\displaystyle R={\frac {1}{2}}{\sqrt {11+4{\sqrt {5}}}}\;a\approx 2{,}2329505a;}$

радиус полувписанной сферы (касающейся всех рёбер в их серединах) —

${\displaystyle \rho ={\frac {1}{2}}{\sqrt {10+4{\sqrt {5}}}}\;a\approx 2{,}1762509a.}$

Примечания

Ссылки

• Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .